Deviasi berarti seberapa jauh dari normal atau rata-rata.
Kita dapat menggunakan standar deviasi untuk mengetahui apakah perilaku tertentu normal atau unik/luar biasa. Standar deviasi sering dihitung dengan rata-rata kumpulan data, dan ini membantu kita untuk mengetahui seberapa tersebar data tersebut. Dengan kata lain, dalam satu set data standar deviasi memberi tahu kita seberapa erat semua titik data yang beragam dikelompokkan di sekitar rata-rata. Standar deviasi dilambangkan dengan simbol \('\sigma'\) .
Deviasi standar dapat dengan mudah dihitung menggunakan kalkulator, perangkat lunak spreadsheet, atau rumus matematika yang dijelaskan di bawah ini.
Mari kita ambil contoh untuk memahaminya dengan lebih baik. Mari kita hitung jumlah buah yang dimiliki tetangga Anda di rumahnya.
| Tetangga | Jumlah buah ( X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Maria | 7 |
| Kim | 9 |
Jumlah buah adalah titik data yang dilambangkan dengan x dan Mean diwakili oleh \(\bar{x}\) . Berarti untuk data di atas adalah
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Sekarang bentuk tabel yang menunjukkan titik data( \(x\) ) , rata-rata ( \(\bar{x}\) dan selisih titik data dari rata-rata( \(x - \bar{x}\)
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Temukan rata-rata selisihnya \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Deviasi Standar:
\(\sigma = \sqrt{4.56} = 2.13\)
Rata-rata = 5,8 buah
Standar Deviasi = 2,13 buah
Sekarang kita dapat dengan mudah mengetahui siapa yang berada dalam satu standar deviasi dan siapa yang berada di luarnya. Jadi standar deviasi membantu kita mengetahui apa itu kasus normal dan apa itu kasus luar biasa.
Kita dapat mengharapkan sekitar dua pertiga data berada dalam +1 atau -1 standar deviasi dari rata-rata. Kita dapat mengatakan \(\frac{2}{3}^{rd}\) tetangga memiliki antara 7,93(5,8 + 2,13) dan 3,67 (5,8 - 2,13) buah di rumah mereka.
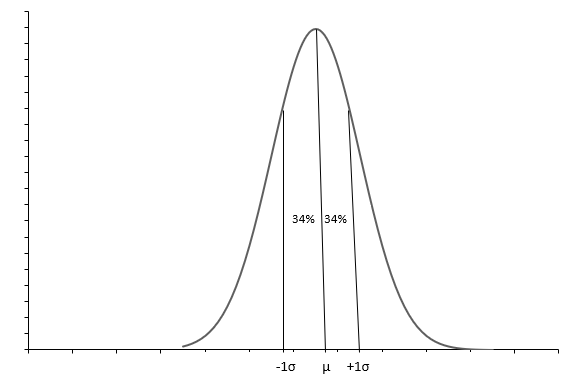
Grafik di atas menunjukkan distribusi normal dengan kurva berbentuk lonceng. Setiap distribusi Normal didefinisikan dengan rata-rata ( \(\mu\) ) dan standar deviasi ( \(\sigma\) ). Kira-kira 68% pengamatan berada di antara \(+1\sigma\) dan \(-1\sigma\) . Mean( \(\mu\) ) juga median memberi tahu kita titik tengah distribusi, di mana semua nilai data tersebar. Standar deviasi( \(\sigma\) ) memberi tahu kita cara menyebarkan data.
Untuk menghitung standar deviasi ikuti langkah-langkah di bawah ini:
1) Temukan rata-rata ( \(\bar{x}\) ) dari item data dalam set yang diberikan
2) Ambil setiap selisih item data dari rata-ratanya, kuadratkan, lalu rata-ratakan hasilnya. Hasil ini disebut Varians
3) Ambil akar kuadrat dari Varians, ini akan memberikan Standar Deviasi \(\sigma\)