Deviazione significa quanto lontano dal normale o dalla media.
Possiamo usare la deviazione standard per sapere se un determinato comportamento è normale o unico/straordinario. La deviazione standard viene spesso calcolata con la media di un set di dati e ci aiuta a sapere quanto sono distribuiti i dati. In altre parole, in un insieme di dati la deviazione standard ci dice quanto strettamente tutti i vari punti dati sono raggruppati attorno alla media. La deviazione standard è indicata dal simbolo \('\sigma'\) .
La deviazione standard può essere facilmente calcolata utilizzando una calcolatrice, un foglio di calcolo o formule matematiche spiegate di seguito.
Facciamo un esempio per capirlo meglio. Teniamo conto del numero di frutti che i tuoi vicini hanno in casa.
| Vicino | N. di frutti ( X) |
| Sam | 3 |
| Daniele | 4 |
| Pettirosso | 6 |
| Maria | 7 |
| Kim | 9 |
Il numero di frutti sono punti dati che sono indicati da x e Mean è rappresentato da \(\bar{x}\) . La media per i dati di cui sopra è
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Ora forma una tabella che mostri i punti dati ( \(x\) ) , la media ( \(\bar{x}\) ) e la differenza del punto dati dalla media ( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Trova la media delle differenze \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Deviazione standard:
\(\sigma = \sqrt{4.56} = 2.13\)
Media = 5,8 frutti
Deviazione standard = 2,13 frutti
Ora possiamo facilmente capire chi è all'interno di una deviazione standard e chi è oltre. Quindi la deviazione standard ci aiuta a sapere quali sono i casi normali e quali i casi straordinari.
Possiamo aspettarci che circa due terzi dei dati rientrino in una deviazione standard di +1 o -1 dalla media. Possiamo dire che \(\frac{2}{3}^{rd}\) dei vicini ha tra 7.93(5.8 + 2.13) e 3.67 (5.8 - 2.13) frutti nelle loro case.
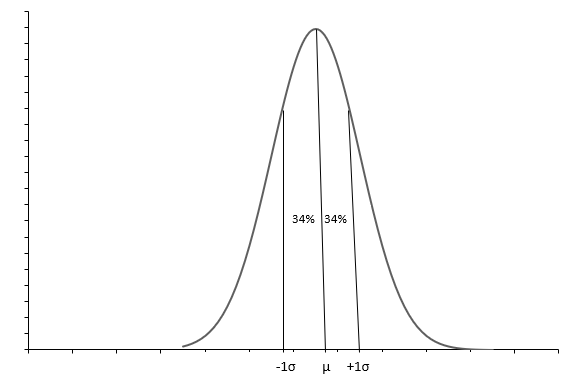
Il grafico sopra mostra una distribuzione normale con una curva a campana. Ogni distribuzione Normale è definita con la media( \(\mu\) ) e la deviazione standard( \(\sigma\) ). Circa il 68% delle osservazioni rientra tra \(+1\sigma\) e \(-1\sigma\) . La media( \(\mu\) ) anche la mediana ci dice il punto medio della distribuzione, attorno al quale sono distribuiti tutti i valori dei dati. La deviazione standard( \(\sigma\) ) ci dice come distribuire i dati.
Per calcolare la deviazione standard seguire i passaggi seguenti:
1) Trova la media( \(\bar{x}\) ) degli elementi di dati nell'insieme dato
2) Prendere ogni differenza di elemento di dati dalla media, elevarla al quadrato e quindi calcolare la media del risultato. Questo risultato si chiama varianza
3) Prendi la radice quadrata della varianza, questo darà la deviazione standard \(\sigma\)