偏差とは、通常または平均からの距離を意味します。
標準偏差を使用して、特定の行動が正常なのか、それとも独特/異常なのかを知ることができます。標準偏差は多くの場合、データ セットの平均値を使用して計算され、データがどの程度分散しているかを知るのに役立ちます。言い換えれば、一連のデータの標準偏差は、さまざまなデータ ポイントがすべて平均値の周りにどの程度密集しているかを示します。標準偏差は記号\('\sigma'\)で表されます。
標準偏差は、電卓、表計算ソフトウェア、または以下で説明する数式を使用して簡単に計算できます。
理解を深めるために例を挙げてみましょう。あなたの隣人が家に持っている果物の数を考えてみましょう。
| 近所の人 | 果物の数 ( X) |
| サム | 3 |
| ダニエル | 4 |
| ロビン | 6 |
| メアリー | 7 |
| キム | 9 |
果物の数は x で示されるデータ ポイントであり、平均は\(\bar{x}\)で表されます。上記のデータの平均は
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
ここで、データ ポイント ( \(x\) ) 、平均 ( \(\bar{x}\) )、および平均からのデータ ポイントの差 ( \(x - \bar{x}\) ) ) を示すテーブルを形成します。
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
差の平均を求めます\(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
標準偏差:
\(\sigma = \sqrt{4.56} = 2.13\)
平均 = 5.8 個の果物
標準偏差 = 2.13 果物
これで、誰が 1 つの標準偏差内にあり、誰がそれを超えているかを簡単に把握できます。したがって、標準偏差は、正常なケースと異常なケースを知るのに役立ちます。
データの約 3 分の 2 が、平均から +1 または -1 の標準偏差内に収まると予想できます。 \(\frac{2}{3}^{rd}\)人の隣人が、家に 7.93(5.8 + 2.13) から 3.67 (5.8 - 2.13) の果物を持っていると言えます。
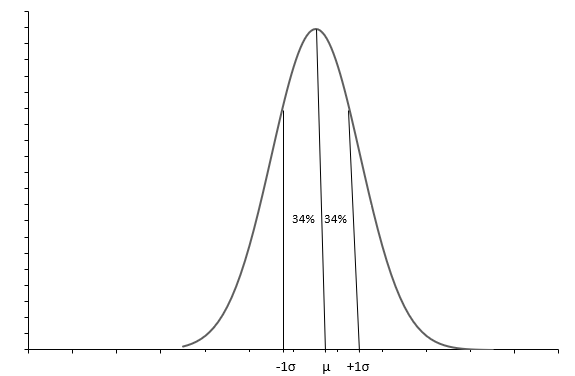
上のグラフは、釣鐘型の曲線を持つ正規分布を示しています。各正規分布は、平均 ( \(\mu\) ) と標準偏差 ( \(\sigma\) ) で定義されます。観測値の約 68% が\(+1\sigma\)と\(-1\sigma\)の間にあります。平均 ( \(\mu\) ) も中央値は、すべてのデータ値が広がっている分布の中点を示します。標準偏差 ( \(\sigma\) ) は、データをどのように分散させるかを示しています。
標準偏差を計算するには、次の手順に従います。
1) 指定されたセット内のデータ項目の平均 ( \(\bar{x}\) ) を見つける
2) データ項目のそれぞれの差を平均から取り、それを 2 乗し、結果を平均します。この結果は分散と呼ばれます
3) 分散の平方根を取ると、標準偏差\(\sigma\)が得られます。