Отстапувањето значи колку далеку од нормалното или просечното.
Можеме да користиме стандардно отстапување за да знаеме дали одредено однесување е нормално или единствено/извонредно. Стандардното отстапување често се пресметува со средната вредност на збир на податоци и ни помага да знаеме колку се распространети податоците. Со други зборови, во збир на податоци стандардното отстапување ни кажува колку цврсто сите различни точки на податоци се групирани околу средната вредност. Стандардната девијација се означува со симболот \('\sigma'\) .
Стандардното отстапување лесно може да се пресмета со помош на калкулатор, софтвер за табеларни пресметки или математички формули кои се објаснети подолу.
Да земеме пример за подобро да го разбереме. Ајде да го земеме предвид бројот на плодови што ги имаат вашите соседи во нивните куќи.
| Соседот | Број на овошје (X) |
| Сем | 3 |
| Даниел | 4 |
| Робин | 6 |
| Мери | 7 |
| Ким | 9 |
Бројот на плодови се податочни точки кои се означени со x, а Средната вредност е претставена со \(\bar{x}\) . Средството за горенаведените податоци е
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Сега формирајте табела која ги прикажува точките на податоци ( \(x\) ), средната вредност ( \(\bar{x}\) ) и разликата на податочната точка од средната вредност ( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7,84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Најдете ја средната вредност на разликите \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Стандардна девијација:
\(\sigma = \sqrt{4.56} = 2.13\)
Средно = 5,8 плодови
Стандардна девијација = 2,13 плодови
Сега лесно можеме да откриеме кои се во рамките на една стандардна девијација и кои се надвор од неа. Значи, стандардното отстапување ни помага да знаеме што се нормални случаи, а што се вонредни случаи.
Можеме да очекуваме околу две третини од податоците да спаѓаат во +1 или -1 стандардно отстапување од средната вредност. Можеме да кажеме дека \(\frac{2}{3}^{rd}\) од соседите имаат помеѓу 7,93 (5,8 + 2,13) и 3,67 (5,8 - 2,13) плодови во нивните куќи.
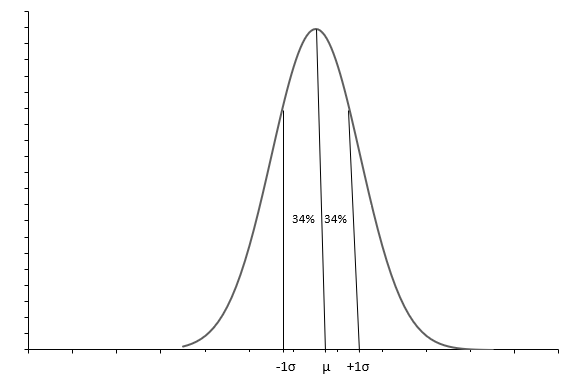
Горенаведениот график покажува нормална дистрибуција со крива на ѕвонче. Секоја Нормална дистрибуција е дефинирана со средна ( \(\mu\) ) и стандардна девијација ( \(\sigma\) ). Приближно 68% од набљудувањата паѓаат помеѓу \(+1\sigma\) и \(-1\sigma\) . Средната вредност ( \(\mu\) ) и медијаната ни ја кажува средната точка на дистрибуцијата, околу која се распоредени сите вредности на податоците. Стандардната девијација ( \(\sigma\) ) ни кажува како да ги рашириме податоците.
За да го пресметате стандардното отстапување, следете ги следниве чекори:
1) Најдете ја средната вредност ( \(\bar{x}\) ) на податочните ставки во даденото множество
2) Земете ја секоја разлика во податочната ставка од средната вредност, квадратете ја, а потоа просечете го резултатот. Овој резултат се нарекува варијанса
3) Земете го квадратниот корен на варијансата, ова ќе даде стандардна девијација \(\sigma\)