Хазайлт нь хэвийн болон дунджаас хэр хол байгааг хэлнэ.
Бид тодорхой зан үйл хэвийн эсвэл өвөрмөц/ер бусын эсэхийг мэдэхийн тулд стандарт хазайлтыг ашиглаж болно. Стандарт хазайлтыг ихэвчлэн өгөгдлийн багцын дундажаар тооцдог бөгөөд энэ нь өгөгдөл хэр тархаж байгааг мэдэхэд тусалдаг. Өөрөөр хэлбэл, өгөгдлийн багц дахь стандарт хазайлт нь бүх янз бүрийн өгөгдлийн цэгүүд дундаж утгын эргэн тойронд хэр нягт бөөгнөрөлдгийг хэлж өгдөг. Стандарт хазайлтыг \('\sigma'\) тэмдгээр тэмдэглэнэ.
Стандарт хазайлтыг тооцоолуур, хүснэгтийн программ хангамж эсвэл доор тайлбарласан математикийн томъёог ашиглан хялбархан тооцоолж болно.
Үүнийг илүү сайн ойлгохын тулд жишээ татъя. Хөршүүдийнхээ гэрт байгаа жимсний тоог авч үзье.
| Хөрш | жимсний тоо ( X) |
| Сэм | 3 |
| Даниел | 4 |
| Робин | 6 |
| Мэри | 7 |
| Ким | 9 |
Жимсний тоо нь өгөгдлийн цэгүүд бөгөөд үүнийг х, дундаж утгыг \(\bar{x}\) -р илэрхийлнэ. Дээрх өгөгдлийн дундаж нь
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Одоо өгөгдлийн цэгүүд( \(x\) ) , дундаж ( \(\bar{x}\) ) болон өгөгдлийн цэгийн дундажаас( \(x - \bar{x}\) ) зөрүүг харуулсан хүснэгт үүсгэ.
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Зөрүүний дундажийг олоорой \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Стандарт хэлбэлзэл:
\(\sigma = \sqrt{4.56} = 2.13\)
Дундаж = 5.8 жимс
Стандарт хазайлт = 2.13 жимс
Одоо бид хэн нэг стандарт хазайлт дотор байгаа, хэн нь түүнээс давж байгааг хялбархан тодорхойлох боломжтой. Тиймээс стандарт хазайлт нь юу нь ердийн тохиолдол, юу нь онцгой тохиолдол болохыг мэдэхэд тусалдаг.
Өгөгдлийн гуравны хоёр нь дунджаас +1 эсвэл -1 стандарт хазайлтад багтана гэж бид найдаж болно. Хөршүүдийн \(\frac{2}{3}^{rd}\) байшинд 7.93(5.8 + 2.13)-аас 3.67 (5.8 - 2.13) жимс байдаг гэж бид хэлж чадна.
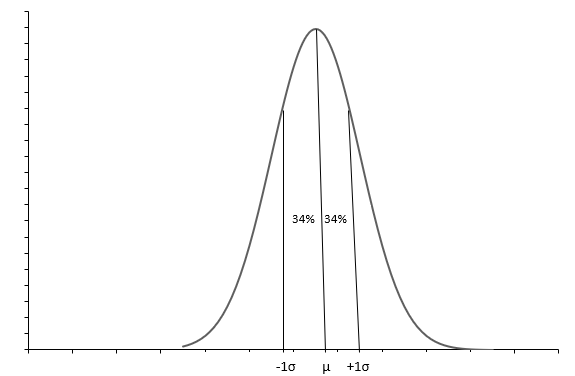
Дээрх график нь хонхны хэлбэрийн муруйтай хэвийн тархалтыг харуулж байна. Хэвийн тархалт бүр нь дундаж ( \(\mu\) ) ба стандарт хазайлтаар ( \(\sigma\) ) тодорхойлогддог. Ажиглалтын 68 орчим хувь нь \(+1\sigma\) ба \(-1\sigma\) хооронд байна. Дундаж ( \(\mu\) ) нь мөн медиан нь бүх өгөгдлийн утгууд тархсан тархалтын дунд цэгийг хэлж өгдөг. Стандарт хазайлт ( \(\sigma\) ) нь өгөгдлийг хэрхэн тараахыг бидэнд хэлдэг.
Стандарт хазайлтыг тооцоолохын тулд дараах алхмуудыг дагана уу.
1) Өгөгдсөн багц дахь өгөгдлийн зүйлийн дундажийг ( \(\bar{x}\) ) ол
2) Өгөгдлийн зүйлийн зөрүү бүрийг дунджаас авч, квадрат болгож, үр дүнг нь дундажлана. Энэ үр дүнг Variance гэж нэрлэдэг
3) Вариацын квадрат язгуурыг авбал стандарт хазайлт \(\sigma\) болно.