သွေဖည်ခြင်းဆိုသည်မှာ ပုံမှန် သို့မဟုတ် ပျမ်းမျှနှင့် မည်မျှဝေးကွာသည်ကို ဆိုလိုသည်။
အချို့သောအပြုအမူများသည် ပုံမှန် သို့မဟုတ် ထူးခြားသည်/သာလွန်ကောင်းမွန်ခြင်းရှိမရှိ သိရှိရန် စံသွေဖည်မှုကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည်။ စံသွေဖည်မှုကို ဒေတာအစုတစ်ခု၏ ဆိုလိုရင်းဖြင့် တွက်ချက်လေ့ရှိပြီး ၎င်းသည် ကျွန်ုပ်တို့အား ဒေတာမည်မျှပျံ့နှံ့နေသည်ကို သိရှိရန် ကူညီပေးသည်။ တစ်နည်းဆိုရသော်၊ ဒေတာစံသွေဖည်မှုအစုတစ်ခုတွင် အမျိုးမျိုးသောဒေတာအချက်များအားလုံးသည် ဆိုလိုရင်းတစ်ဝိုက်တွင် မည်မျှတင်းကျပ်စွာ အစုလိုက်အပြုံလိုက်ရှိသည်ကို ပြောပြသည်။ စံသွေဖည်မှုကို သင်္ကေတ \('\sigma'\) ဖြင့် ဖော်ပြသည်။
အောက်တွင်ရှင်းပြထားသည့် ဂဏန်းပေါင်းစက်၊ စာရင်းဇယားဆော့ဖ်ဝဲ သို့မဟုတ် သင်္ချာဖော်မြူလာများကို အသုံးပြု၍ စံသွေဖည်မှုကို အလွယ်တကူ တွက်ချက်နိုင်သည်။
ပိုနားလည်အောင် ဥပမာတစ်ခုယူကြည့်ရအောင်။ အိမ်နီးနားချင်းတွေရဲ့ အိမ်မှာရှိတဲ့ အသီးအနှံတွေကို တွက်ကြည့်ရအောင်။
| အိမ်နီးချင်း | အသီးအနှံ နံပါတ် (X) |
| ဆမ် | ၃ |
| ဒံယေလ | ၄ |
| ရော်ဘင် | ၆ |
| မေရီ | ၇ |
| ကင် | ၉ |
အသီးအနှံများ၏ အရေအတွက်များသည် x ဖြင့် ဖော်ပြထားသည့် ဒေတာအမှတ်ဖြစ်ပြီး Mean ကို \(\bar{x}\) ဖြင့် ကိုယ်စားပြုသည်။ အထက်ပါ အချက်အလက်များအတွက် ဆိုလိုသည်မှာ
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
ယခု ဒေတာအမှတ်( \(x\) ) ၊ mean \(\bar{x}\) နှင့် mean ( \(x - \bar{x}\) နှင့် ဒေတာအမှတ် ကွာခြားချက်ကို ပြသသည့် ဇယားကို ဖွဲ့ပါ။
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| ၃ | ၅.၈ | ၇.၈၄ |
| ၄ | ၅.၈ | ၃.၂၄ |
| ၆ | ၅.၈ | ၀.၀၄ |
| ၇ | ၅.၈ | ၁.၄၄ |
| ၉ | ၅.၈ | ၁၀.၂၄ |
ကွာခြားချက်များ၏ ဆိုလိုရင်းကို ရှာပါ \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
စံသွေဖည်မှု-
\(\sigma = \sqrt{4.56} = 2.13\)
အသီးအနှံ = ၅.၈
Standard Deviation = 2.13 အသီးအနှံများ
ယခု ကျွန်ုပ်တို့သည် စံသွေဖည်မှုတစ်ခုအတွင်း မည်သူနှင့် ၎င်းထက်ကျော်လွန်နေကြောင်း အလွယ်တကူ ရှာဖွေတွေ့ရှိနိုင်ပြီဖြစ်သည်။ ထို့ကြောင့် စံသွေဖည်မှုမှာ သာမန်ကိစ္စများနှင့် ထူးကဲသောကိစ္စများဖြစ်သည်ကို သိရန် ကူညီပေးသည်။
ဒေတာ၏သုံးပုံနှစ်ပုံခန့်သည် +1 သို့မဟုတ် -1 စံသွေဖည်မှုအတွင်း ကျဆင်းရန်မျှော်လင့်နိုင်သည်။ အိမ်နီးနားချင်းများ၏ \(\frac{2}{3}^{rd}\) အိမ်တွင် 7.93(5.8 + 2.13) နှင့် 3.67 (5.8 - 2.13) ကြား အသီးအနှံများ ရှိသည်ဟု ဆိုနိုင်ပါသည်။
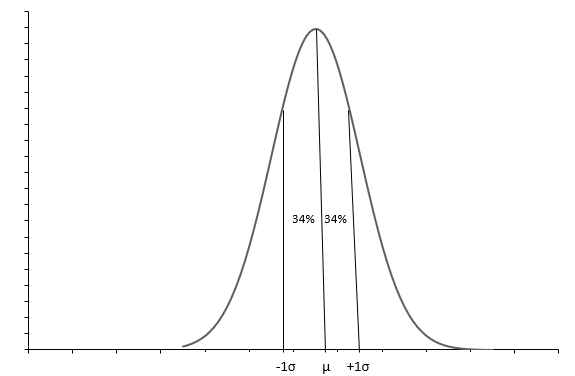
အထက်ဖော်ပြပါ ဂရပ်သည် ခေါင်းလောင်းပုံသဏ္ဍာန်မျဉ်းကွေးဖြင့် ပုံမှန်ဖြန့်ဝေမှုကို ပြသသည်။ ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုစီကို ပျမ်းမျှ( \(\mu\) ) နှင့် စံသွေဖည်မှု( \(\sigma\) ) ဖြင့် သတ်မှတ်သည်။ ခန့်မှန်းခြေ 68% သည် \(+1\sigma\) နှင့် \(-1\sigma\) ကြားတွင် ရှိသည်။ ပျမ်းမျှ( \(\mu\) ) သည် ဒေတာတန်ဖိုးများ ပျံ့နှံ့နေသည့် အနီးတစ်ဝိုက်တွင် ဖြန့်ဖြူးမှု၏ အလယ်ဗဟိုအချက်ကိုလည်း ပြောပြသည်။ စံသွေဖည်မှု( \(\sigma\) ) သည် ဒေတာကို မည်သို့ဖြန့်ထုတ်ရမည်ကို ပြောပြသည်။
စံသွေဖည်မှုကို တွက်ချက်ရန် အောက်ပါ အဆင့်များကို လိုက်နာပါ ။
1) ပေးထားသော set အတွင်းရှိ data items များ၏ mean( \(\bar{x}\) ကိုရှာပါ။
2) ဒေတာအကြောင်းအရာ၏ ကွာခြားချက်တစ်ခုစီကို ပျမ်းမျှအနေဖြင့် ယူပါ၊ ၎င်းကို နှစ်ထပ်ချပြီးနောက် ရလဒ်ကို ပျမ်းမျှ။ ဤရလဒ်ကို Variance ဟုခေါ်သည်။
3) Variance ၏ နှစ်ထပ်ကိန်းကိုယူပါ၊ ၎င်းသည် Standard Deviation \(\sigma\) ကိုပေးလိမ့်မည်။