विचलन भनेको सामान्य वा औसतबाट कति टाढा हुन्छ भन्ने बुझिन्छ।
हामीले मानक विचलन प्रयोग गर्न सक्छौं कि निश्चित व्यवहार सामान्य वा अद्वितीय/असाधारण छ। मानक विचलन प्रायः डेटा सेटको माध्यमबाट गणना गरिन्छ, र यसले हामीलाई डेटा कसरी फैलिएको छ भनेर जान्न मद्दत गर्दछ। अन्य शब्दहरूमा, डेटाको सेटमा मानक विचलनले हामीलाई बताउँछ कि सबै विभिन्न डेटा बिन्दुहरू औसत वरिपरि क्लस्टर गरिएका छन्। मानक विचलन प्रतीक \('\sigma'\) द्वारा जनाइएको छ।
मानक विचलन सजिलैसँग क्याल्कुलेटर, स्प्रेडसिट सफ्टवेयर वा तल व्याख्या गरिएका गणित सूत्रहरू प्रयोग गरेर गणना गर्न सकिन्छ।
यसलाई राम्रोसँग बुझ्नको लागि एउटा उदाहरण लिऔं। तपाईंको छिमेकीहरूको घरमा कति फलफूल छन् भन्ने हिसाब गरौं।
| छिमेकी | फलफूलको संख्या (X) |
| साम | ३ |
| डेनियल | ४ |
| रोबिन | ६ |
| मेरी | ७ |
| किम | ९ |
फलहरूको संख्या डेटा बिन्दुहरू हुन् जुन x द्वारा जनाइएको छ र मतलब \(\bar{x}\) द्वारा प्रतिनिधित्व गरिन्छ। माथिको डाटाको लागि मतलब छ
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
अब एउटा तालिका बनाउनुहोस् जसले डेटा बिन्दुहरू ( \(x\) ) , मतलब ( \(\bar{x}\) ) र माध्य ( \(x - \bar{x}\) बाट डेटा बिन्दुको भिन्नता देखाउँछ।
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| ३ | ५.८ | ७.८४ |
| ४ | ५.८ | ३.२४ |
| ६ | ५.८ | ०.०४ |
| ७ | ५.८ | १.४४ |
| ९ | ५.८ | १०.२४ |
भिन्नताहरूको औसत पत्ता लगाउनुहोस् \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
मानक विचलन:
\(\sigma = \sqrt{4.56} = 2.13\)
औसत = 5.8 फल
मानक विचलन = 2.13 फल
अब हामी सजिलै पत्ता लगाउन सक्छौं कि को एक मानक विचलन भित्र छन् र को यो भन्दा पर छन्। त्यसैले मानक विचलनले हामीलाई सामान्य केसहरू के हुन् र असाधारण केसहरू के हुन् भनेर जान्न मद्दत गर्दछ।
हामीले करिब दुई तिहाई डेटा औसतबाट +1 वा -1 मानक विचलन भित्र आउने आशा गर्न सक्छौं। हामी भन्न सक्छौं \(\frac{2}{3}^{rd}\) छिमेकीहरूको घरमा 7.93 (5.8 + 2.13) र 3.67 (5.8 - 2.13) बीचको फलहरू छन्।
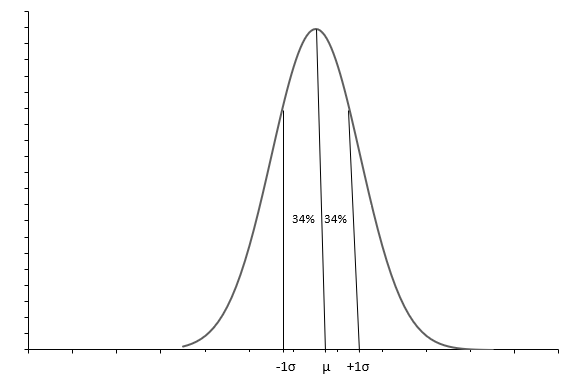
माथिको ग्राफले घण्टी आकार वक्रको साथ सामान्य वितरण देखाउँछ। प्रत्येक सामान्य वितरण मतलब ( \(\mu\) ) र मानक विचलन ( \(\sigma\) ) सँग परिभाषित गरिएको छ। लगभग 68% अवलोकनहरू \(+1\sigma\) र \(-1\sigma\) बीचमा आउँछन्। माध्य ( \(\mu\) ) ले पनि हामीलाई वितरणको मध्य बिन्दु बताउँछ, जसको वरिपरि सबै डेटा मानहरू फैलिएका छन्। मानक विचलन ( \(\sigma\) ) ले हामीलाई डेटा कसरी फैलाउने भनेर बताउँछ।
मानक विचलन गणना गर्न निम्न चरणहरू पालना गर्नुहोस्:
1) दिइएको सेटमा डेटा वस्तुहरूको मतलब ( \(\bar{x}\) फेला पार्नुहोस्
2) डेटा वस्तुको प्रत्येक भिन्नतालाई औसतबाट लिनुहोस्, यसलाई वर्ग गर्नुहोस्, र त्यसपछि परिणामको औसत गर्नुहोस्। यस परिणामलाई भिन्नता भनिन्छ
3) भिन्नताको वर्गमूल लिनुहोस्, यसले मानक विचलन दिन्छ \(\sigma\)