Afwijking betekent hoe ver van het normale of gemiddelde.
We kunnen standaarddeviatie gebruiken om te weten of bepaald gedrag normaal of uniek/buitengewoon is. Standaarddeviatie wordt vaak berekend met het gemiddelde van een dataset, en het helpt ons te weten hoe verspreid de data is. Met andere woorden, in een reeks gegevens vertelt de standaarddeviatie ons hoe strak alle verschillende gegevenspunten rond het gemiddelde zijn geclusterd. Standaarddeviatie wordt aangegeven met het symbool \('\sigma'\) .
De standaarddeviatie kan eenvoudig worden berekend met behulp van een rekenmachine, spreadsheetsoftware of wiskundige formules die hieronder worden uitgelegd.
Laten we een voorbeeld nemen om het beter te begrijpen. Laten we rekening houden met het aantal vruchten dat je buren in huis hebben.
| Buurman | Aantal vruchten ( X) |
| Sam | 3 |
| Daniël | 4 |
| Robin | 6 |
| Maria | 7 |
| Kim | 9 |
Het aantal vruchten zijn gegevenspunten die worden aangegeven met x en het gemiddelde wordt weergegeven door \(\bar{x}\) . Het gemiddelde voor de bovenstaande gegevens is:
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Vorm nu een tabel met gegevenspunten( \(x\) ) , gemiddelde ( \(\bar{x}\) ) en het verschil tussen het gegevenspunt en het gemiddelde( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Zoek het gemiddelde van de verschillen \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Standaardafwijking:
\(\sigma = \sqrt{4.56} = 2.13\)
Gemiddelde = 5,8 fruit
Standaarddeviatie = 2.13 vruchten
Nu kunnen we gemakkelijk achterhalen wie binnen één standaarddeviatie vallen en wie daarbuiten. Dus standaarddeviatie helpt ons om te weten wat normale gevallen zijn en wat buitengewone gevallen.
We kunnen verwachten dat ongeveer tweederde van de gegevens binnen +1 of -1 standaarddeviatie van het gemiddelde valt. We kunnen zeggen dat \(\frac{2}{3}^{rd}\) van buren tussen 7,93 (5,8 + 2,13) en 3,67 (5,8 - 2,13) fruit in huis hebben.
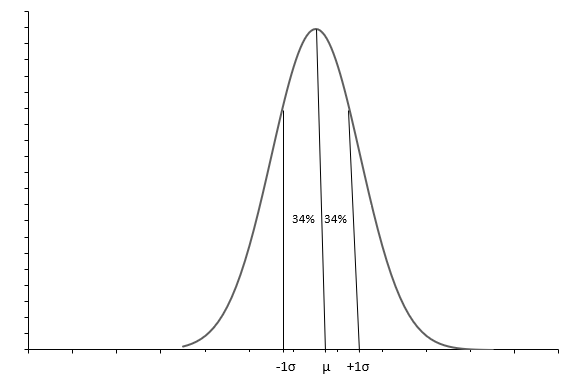
De bovenstaande grafiek toont een normale verdeling met een klokvormige curve. Elke normale verdeling wordt gedefinieerd met het gemiddelde( \(\mu\) ) en standaarddeviatie( \(\sigma\) ). Ongeveer 68% van de waarnemingen valt tussen \(+1\sigma\) en \(-1\sigma\) . Het gemiddelde( \(\mu\) ) ook de mediaan vertelt ons het middelpunt van de verdeling, waarrond alle gegevenswaarden zijn verspreid. Standaarddeviatie( \(\sigma\) ) vertelt ons hoe we de gegevens moeten spreiden.
Volg de onderstaande stappen om de standaarddeviatie te berekenen:
1) Vind gemiddelde ( \(\bar{x}\) ) van de gegevensitems in de gegeven set
2) Neem elk verschil van het gegevensitem van het gemiddelde, kwadratisch en neem vervolgens het gemiddelde van het resultaat. Dit resultaat heet Variantie
3) Neem de vierkantswortel van de variantie, dit geeft de standaarddeviatie \(\sigma\)