Odchylenie oznacza, jak daleko od normy lub średniej.
Możemy użyć odchylenia standardowego, aby wiedzieć, czy określone zachowanie jest normalne, czy wyjątkowe/nadzwyczajne. Odchylenie standardowe jest często obliczane na podstawie zbioru danych i pomaga nam dowiedzieć się, jak rozłożone są dane. Innymi słowy, w zbiorze danych odchylenie standardowe mówi nam, jak ściśle wszystkie różne punkty danych są skupione wokół średniej. Odchylenie standardowe jest oznaczone symbolem \('\sigma'\) .
Odchylenie standardowe można łatwo obliczyć za pomocą kalkulatora, arkusza kalkulacyjnego lub formuł matematycznych, które wyjaśniono poniżej.
Weźmy przykład, aby lepiej to zrozumieć. Weźmy pod uwagę liczbę owoców, które twoi sąsiedzi mają w swoich domach.
| Sąsiad | Ilość owoców (X) |
| Sama | 3 |
| Danielu | 4 |
| Rudzik | 6 |
| Maryja | 7 |
| Kim | 9 |
Liczba owoców to punkty danych, które są oznaczone przez x, a średnia jest reprezentowana przez \(\bar{x}\) . Średnia dla powyższych danych to
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Teraz utwórz tabelę, która pokazuje punkty danych ( \(x\) ), średnią ( \(\bar{x}\) ) i różnicę punktu danych od średniej ( \(x - \bar{x}\)
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7,84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Znajdź średnią różnic \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Odchylenie standardowe:
\(\sigma = \sqrt{4.56} = 2.13\)
Średnia = 5,8 owoców
Odchylenie standardowe = 2,13 owoców
Teraz możemy łatwo dowiedzieć się, kto mieści się w jednym odchyleniu standardowym, a kto poza nim. Tak więc odchylenie standardowe pomaga nam wiedzieć, które przypadki są normalne, a które nadzwyczajne.
Możemy spodziewać się, że około dwie trzecie danych mieści się w zakresie +1 lub -1 odchylenia standardowego od średniej. Możemy powiedzieć \(\frac{2}{3}^{rd}\) sąsiadów ma w swoich domach od 7,93 (5,8 + 2,13) do 3,67 (5,8 - 2,13) owoców.
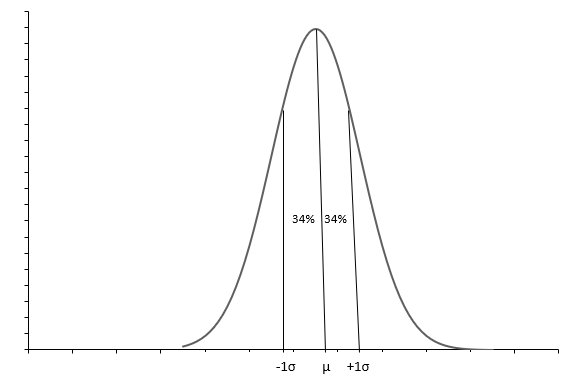
Powyższy wykres przedstawia rozkład normalny z krzywą w kształcie dzwonu. Każdy rozkład normalny jest zdefiniowany za pomocą średniej ( \(\mu\) ) i odchylenia standardowego ( \(\sigma\) ). Około 68% obserwacji mieści się w przedziale od \(+1\sigma\) do \(-1\sigma\) . Średnia ( \(\mu\) ) również mediana mówi nam o środku rozkładu, wokół którego rozłożone są wszystkie wartości danych. Odchylenie standardowe ( \(\sigma\) ) mówi nam, jak rozłożyć dane.
Aby obliczyć odchylenie standardowe, wykonaj poniższe czynności:
1) Znajdź średnią ( \(\bar{x}\) ) elementów danych w danym zbiorze
2) Weź każdą różnicę elementu danych od średniej, podnieś ją do kwadratu, a następnie uśrednij wynik. Ten wynik nazywa się wariancją
3) Weź pierwiastek kwadratowy z Wariancji, to da Odchylenie Standardowe \(\sigma\)