Desvio significa quão longe do normal ou da média.
Podemos usar o desvio padrão para saber se determinado comportamento é normal ou único/extraordinário. O desvio padrão geralmente é calculado com a média de um conjunto de dados e nos ajuda a saber o quão dispersos estão os dados. Em outras palavras, em um conjunto de dados, o desvio padrão nos diz com que precisão todos os vários pontos de dados estão agrupados em torno da média. O desvio padrão é indicado pelo símbolo \('\sigma'\) .
O desvio padrão pode ser facilmente calculado usando uma calculadora, software de planilha ou fórmulas matemáticas que são explicadas abaixo.
Vamos dar um exemplo para entender melhor. Vamos levar em conta o número de frutas que seus vizinhos têm em suas casas.
| Vizinho | Nº de frutas (X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Mary | 7 |
| Kim | 9 |
O número de frutas são pontos de dados que são denotados por x e a Média é representada por \(\bar{x}\) . A média dos dados acima é
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Agora forme uma tabela que mostre os pontos de dados ( \(x\) ), a média ( \(\bar{x}\) ) e a diferença do ponto de dados da média( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5,8 | 7,84 |
| 4 | 5,8 | 3,24 |
| 6 | 5,8 | 0,04 |
| 7 | 5,8 | 1,44 |
| 9 | 5,8 | 10,24 |
Encontre a média das diferenças \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Desvio padrão:
\(\sigma = \sqrt{4.56} = 2.13\)
Média = 5,8 frutas
Desvio Padrão = 2,13 frutas
Agora podemos descobrir facilmente quem está dentro de um desvio padrão e quem está além dele. Então o desvio padrão nos ajuda a saber o que são casos normais e quais são casos extraordinários.
Podemos esperar que cerca de dois terços dos dados caiam dentro de +1 ou -1 desvio padrão da média. Podemos dizer que \(\frac{2}{3}^{rd}\) de vizinhos têm entre 7,93(5,8 + 2,13) e 3,67 (5,8 - 2,13) frutas em suas casas.
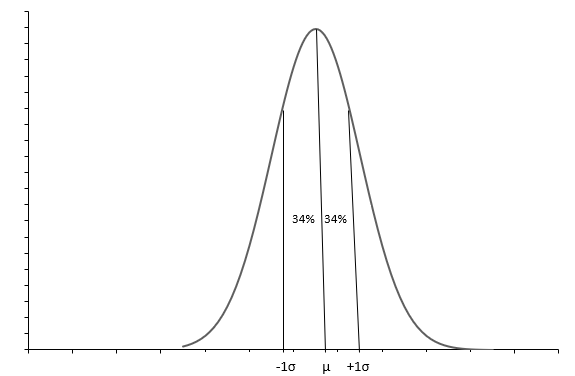
O gráfico acima mostra uma distribuição normal com uma curva em forma de sino. Cada distribuição Normal é definida com a média( \(\mu\) ) e o desvio padrão( \(\sigma\) ). Aproximadamente 68% das observações estão entre \(+1\sigma\) e \(-1\sigma\) . A média( \(\mu\) ) também a mediana nos diz o ponto médio da distribuição, em torno do qual todos os valores de dados estão espalhados. Desvio padrão( \(\sigma\) ) nos diz como distribuir os dados.
Para calcular o desvio padrão siga os passos abaixo:
1) Encontre a média( \(\bar{x}\) ) dos itens de dados no conjunto dado
2) Pegue cada diferença de item de dados da média, eleve ao quadrado e, em seguida, faça a média do resultado. Esse resultado é chamado de Variância
3) Pegue a raiz quadrada da Variância, isso dará o Desvio Padrão \(\sigma\)