Отклонение означает, насколько далеко от нормы или среднего значения.
Мы можем использовать стандартное отклонение, чтобы узнать, является ли определенное поведение нормальным или уникальным/экстраординарным. Стандартное отклонение часто рассчитывается со средним значением набора данных, и это помогает нам узнать, насколько разбросаны данные. Другими словами, в наборе данных стандартное отклонение говорит нам, насколько плотно все различные точки данных сгруппированы вокруг среднего значения. Стандартное отклонение обозначается символом \('\sigma'\) .
Стандартное отклонение можно легко рассчитать с помощью калькулятора, программного обеспечения для работы с электронными таблицами или математических формул, которые объясняются ниже.
Давайте возьмем пример, чтобы понять это лучше. Давайте посчитаем, сколько фруктов есть у ваших соседей в домах.
| Сосед | Количество фруктов ( X ) |
| Сэм | 3 |
| Даниэль | 4 |
| Робин | 6 |
| Мэри | 7 |
| Ким | 9 |
Количество фруктов - это точки данных, которые обозначаются x, а среднее значение представлено \(\bar{x}\) . Среднее значение для приведенных выше данных
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Теперь сформируйте таблицу, которая показывает точки данных ( \(x\) ), среднее значение ( \(\bar{x}\) ) и отличие точки данных от среднего ( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5,8 | 7,84 |
| 4 | 5,8 | 3,24 |
| 6 | 5,8 | 0,04 |
| 7 | 5,8 | 1,44 |
| 9 | 5,8 | 10.24 |
Найдите среднее значение разностей \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Стандартное отклонение:
\(\sigma = \sqrt{4.56} = 2.13\)
Среднее значение = 5,8 плодов
Стандартное отклонение = 2,13 плода.
Теперь мы можем легко выяснить, кто находится в пределах одного стандартного отклонения, а кто за его пределами. Таким образом, стандартное отклонение помогает нам узнать, что является нормальным, а что экстраординарным.
Мы можем ожидать, что около двух третей данных будут находиться в пределах +1 или -1 стандартного отклонения от среднего значения. Мы можем сказать, что \(\frac{2}{3}^{rd}\) соседей имеют в своих домах от 7,93 (5,8 + 2,13) до 3,67 (5,8 - 2,13) фруктов.
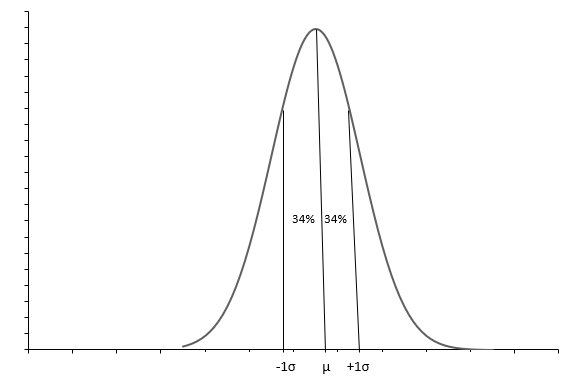
На приведенном выше графике показано нормальное распределение с колоколообразной кривой. Каждое нормальное распределение определяется средним значением ( \(\mu\) ) и стандартным отклонением ( \(\sigma\) ). Приблизительно 68% наблюдений попадают между \(+1\sigma\) и \(-1\sigma\) . Среднее ( \(\mu\) ) также медиана указывает нам среднюю точку распределения, вокруг которой разбросаны все значения данных. Стандартное отклонение ( \(\sigma\) ) говорит нам, как распределить данные.
Для расчета стандартного отклонения выполните следующие шаги:
1) Найдите среднее ( \(\bar{x}\) ) элементов данных в заданном наборе
2) Возьмите каждое отличие элемента данных от среднего, возведите его в квадрат, а затем усредните результат. Этот результат называется дисперсией
3) Возьмите квадратный корень из дисперсии, это даст стандартное отклонение \(\sigma\)