Devijimi do të thotë sa larg nga normalja ose mesatarja.
Ne mund të përdorim devijimin standard për të ditur nëse një sjellje e caktuar është normale apo unike/e jashtëzakonshme. Devijimi standard shpesh llogaritet me mesataren e një grupi të dhënash dhe na ndihmon të dimë se sa të përhapura janë të dhënat. Me fjalë të tjera, në një grup të dhënash devijimi standard na tregon se sa fort janë të grumbulluara të gjitha pikat e ndryshme të të dhënave rreth mesatares. Devijimi standard shënohet me simbolin \('\sigma'\) .
Devijimi standard mund të llogaritet lehtësisht duke përdorur një kalkulator, softuer të fletëllogaritjes ose formula matematikore që shpjegohen më poshtë.
Le të marrim një shembull për ta kuptuar më mirë. Le të marrim parasysh numrin e frutave që fqinjët tuaj kanë në shtëpitë e tyre.
| Komshiu | Numri i frutave (X) |
| Sam | 3 |
| Danieli | 4 |
| Robin | 6 |
| Maria | 7 |
| Kim | 9 |
Numri i frutave janë pika të dhënash të cilat shënohen me x dhe Mesatarja përfaqësohet me \(\bar{x}\) . Mesatarja për të dhënat e mësipërme është
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Tani formoni një tabelë që tregon pikat e të dhënave ( \(x\) ), mesataren ( \(\bar{x}\) ) dhe ndryshimin e pikës së të dhënave nga mesatarja ( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Gjeni mesataren e diferencave \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Devijimi standard:
\(\sigma = \sqrt{4.56} = 2.13\)
Mesatarja = 5.8 fruta
Devijimi standard = 2.13 fruta
Tani mund të kuptojmë lehtësisht se cilët janë brenda një devijimi standard dhe kush janë përtej tij. Pra, devijimi standard na ndihmon të dimë se cilat janë rastet normale dhe cilat janë rastet e jashtëzakonshme.
Mund të presim që rreth dy të tretat e të dhënave të bien brenda devijimit standard +1 ose -1 nga mesatarja. Mund të themi se \(\frac{2}{3}^{rd}\) e fqinjëve kanë midis 7,93 (5,8 + 2,13) dhe 3,67 (5,8 - 2,13) fruta në shtëpitë e tyre.
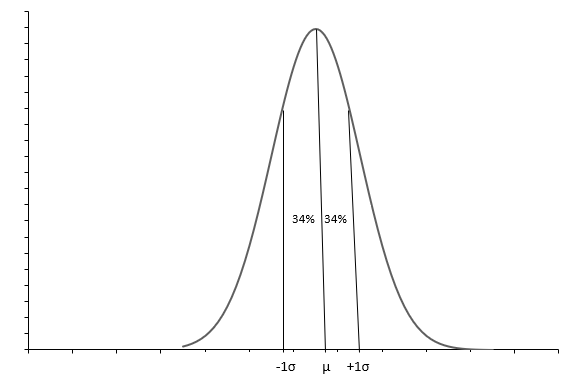
Grafiku i mësipërm tregon një shpërndarje normale me një kurbë në formë zile. Çdo shpërndarje Normale përcaktohet me mesataren( \(\mu\) ) dhe devijimin standard ( \(\sigma\) ). Përafërsisht 68% e vëzhgimeve bien midis \(+1\sigma\) dhe \(-1\sigma\) . Mesatarja ( \(\mu\) ) gjithashtu mediana na tregon pikën e mesit të shpërndarjes, rreth së cilës shpërndahen të gjitha vlerat e të dhënave. Devijimi standard ( \(\sigma\) ) na tregon se si të shpërndajmë të dhënat.
Për të llogaritur devijimin standard, ndiqni hapat e mëposhtëm:
1) Gjeni mesataren ( \(\bar{x}\) ) të artikujve të të dhënave në grupin e dhënë
2) Merrni çdo diferencë të elementit të të dhënave nga mesatarja, katrore atë dhe më pas mesatarizoni rezultatin. Ky rezultat quhet Variancë
3) Merrni rrënjën katrore të Variancës, kjo do të japë Devijimin Standard \(\sigma\)