Avvikelse betyder hur långt från det normala eller genomsnittet.
Vi kan använda standardavvikelse för att veta om ett visst beteende är normalt eller unikt/extraordinärt. Standardavvikelsen beräknas ofta med medelvärdet av en datamängd, och det hjälper oss att veta hur spridda uppgifterna är. Med andra ord, i en uppsättning data berättar standardavvikelsen oss hur tätt alla olika datapunkter är klustrade runt medelvärdet. Standardavvikelsen betecknas med symbolen \('\sigma'\) .
Standardavvikelsen kan enkelt beräknas med hjälp av en miniräknare, kalkylprogram eller matematiska formler som förklaras nedan.
Låt oss ta ett exempel för att förstå det bättre. Låt oss ta hänsyn till antalet frukter som dina grannar har i sina hus.
| Granne | Antal frukter ( X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Mary | 7 |
| Kim | 9 |
Antalet frukter är datapunkter som betecknas med x och medelvärde representeras av \(\bar{x}\) Medelvärdet för ovanstående data är
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Skapa nu en tabell som visar datapunkter( \(x\) ), medelvärde ( \(\bar{x}\) ) och skillnaden mellan datapunkten och medelvärdet( \(x - \bar{x}\)
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7,84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1,44 |
| 9 | 5.8 | 10.24 |
Hitta medelvärdet av skillnaderna \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Standardavvikelse:
\(\sigma = \sqrt{4.56} = 2.13\)
Medelvärde = 5,8 frukter
Standardavvikelse = 2,13 frukter
Nu kan vi enkelt ta reda på vilka som ligger inom en standardavvikelse och vilka som ligger bortom den. Så standardavvikelse hjälper oss att veta vad som är normala fall och vad som är extraordinära fall.
Vi kan förvänta oss att cirka två tredjedelar av data hamnar inom +1 eller -1 standardavvikelse från medelvärdet. Vi kan säga \(\frac{2}{3}^{rd}\) av grannarna har mellan 7,93(5,8 + 2,13) och 3,67 (5,8 - 2,13) frukter i sina hus.
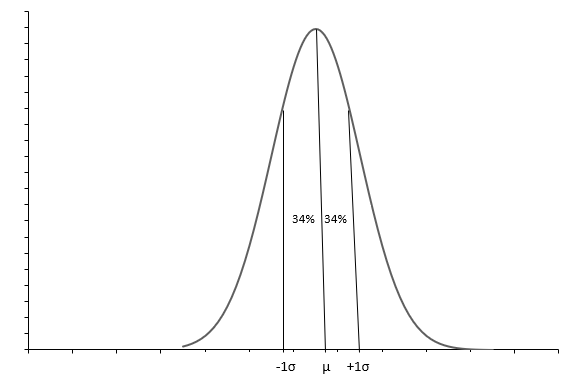
Grafen ovan visar en normalfördelning med en klockformskurva. Varje normalfördelning definieras med medelvärdet( \(\mu\) och standardavvikelsen( \(\sigma\) . Cirka 68 % av observationerna ligger mellan \(+1\sigma\) och \(-1\sigma\) . Medelvärdet ( \(\mu\) också medianen talar om för oss mittpunkten av fördelningen, runt vilken alla datavärden är spridda. Standardavvikelse( \(\sigma\) ) talar om för oss hur man sprider informationen.
Följ stegen nedan för att beräkna standardavvikelsen:
1) Hitta medelvärdet( \(\bar{x}\) ) av dataposterna i den givna uppsättningen
2) Ta varje skillnad mellan dataobjekt från medelvärdet, kvadrera det och sedan genomsnittet av resultatet. Detta resultat kallas Varians
3) Ta kvadratroten av variansen, detta ger standardavvikelse \(\sigma\)