Mkengeuko unamaanisha umbali gani kutoka kwa kawaida au wastani.
Tunaweza kutumia mkengeuko wa kawaida ili kujua kama tabia fulani ni ya kawaida au ya kipekee/isiyo ya kawaida. Mkengeuko wa kawaida mara nyingi huhesabiwa kwa wastani wa seti ya data, na hutusaidia kujua jinsi data ilivyosambazwa. Kwa maneno mengine, katika seti ya ukengeushaji wa kawaida wa data hutuambia jinsi vidokezo vyote vya data vimeunganishwa karibu na wastani. Mkengeuko wa kawaida unaonyeshwa na ishara \('\sigma'\) .
Mkengeuko wa kawaida unaweza kuhesabiwa kwa urahisi kwa kutumia kikokotoo, programu ya lahajedwali au fomula za hesabu ambazo zimefafanuliwa hapa chini.
Hebu tuchukue mfano ili kuelewa vizuri zaidi. Hebu tuzingatie idadi ya matunda ambayo majirani wako wanayo katika nyumba zao.
| Jirani | Idadi ya matunda (X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Mariamu | 7 |
| Kim | 9 |
Idadi ya matunda ni pointi za data ambazo zinaashiria x na Mean inawakilishwa na \(\bar{x}\) . Maana kwa data hapo juu ni
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Sasa tengeneza jedwali linaloonyesha alama za data( \(x\) ) , maana ( \(\bar{x}\) ) na tofauti ya nukta ya data kutoka kwa maana( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Tafuta maana ya tofauti \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Mkengeuko wa Kawaida:
\(\sigma = \sqrt{4.56} = 2.13\)
Wastani = matunda 5.8
Mkengeuko wa Kawaida = matunda 2.13
Sasa tunaweza kubaini kwa urahisi ni nani walio ndani ya mchepuko mmoja wa kawaida na ni nani walio zaidi yake. Kwa hivyo kupotoka kwa kawaida hutusaidia kujua ni kesi gani za kawaida na ni kesi gani za kushangaza.
Tunaweza kutarajia karibu theluthi mbili ya data kuanguka ndani ya +1 au -1 mkengeuko wa kawaida kutoka kwa wastani. Tunaweza kusema \(\frac{2}{3}^{rd}\) ya majirani wana kati ya 7.93(5.8 + 2.13) na 3.67 (5.8 - 2.13) matunda katika nyumba zao.
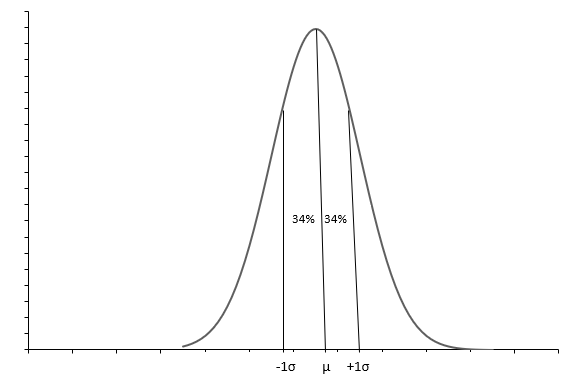
Grafu iliyo hapo juu inaonyesha usambazaji wa kawaida na curve ya umbo la kengele. Kila usambazaji wa Kawaida hufafanuliwa kwa maana( \(\mu\) ) na mchepuko wa kawaida( \(\sigma\) ). Takriban 68% ya uchunguzi huanguka kati ya \(+1\sigma\) na \(-1\sigma\) . The mean( \(\mu\) ) pia wastani hutuambia sehemu ya katikati ya usambazaji, ambapo thamani zote za data zimeenea. Mkengeuko wa kawaida( \(\sigma\) ) hutuambia jinsi ya kueneza data ilivyo.
Ili kuhesabu kupotoka kwa kawaida, fuata hatua zifuatazo:
1) Tafuta maana( \(\bar{x}\) ) ya vitu vya data kwenye seti uliyopewa
2) Chukua kila tofauti ya kipengee cha data kutoka kwa wastani, mraba, na kisha wastani wa matokeo. Matokeo haya yanaitwa Variance
3) Chukua mzizi wa mraba wa Tofauti, hii itatoa Mkengeuko wa Kawaida \(\sigma\)