ค่าเบี่ยงเบนหมายถึงระยะห่างจากค่าปกติหรือค่าเฉลี่ย
เราสามารถใช้ค่าเบี่ยงเบนมาตรฐานเพื่อทราบว่าพฤติกรรมบางอย่างเป็นเรื่องปกติหรือไม่ซ้ำ/พิเศษ ค่าเบี่ยงเบนมาตรฐานมักจะคำนวณด้วยค่าเฉลี่ยของชุดข้อมูล และช่วยให้เราทราบว่าข้อมูลกระจายออกไปอย่างไร กล่าวอีกนัยหนึ่ง ในชุดค่าเบี่ยงเบนมาตรฐานของข้อมูลจะบอกเราว่าจุดข้อมูลต่างๆ รวมกันแน่นแค่ไหนรอบๆ ค่าเฉลี่ย ส่วนเบี่ยงเบนมาตรฐานแสดงด้วยสัญลักษณ์ \('\sigma'\)
ค่าเบี่ยงเบนมาตรฐานสามารถคำนวณได้ง่ายๆ โดยใช้เครื่องคิดเลข ซอฟต์แวร์สเปรดชีต หรือสูตรทางคณิตศาสตร์ที่อธิบายไว้ด้านล่าง
ลองมาดูตัวอย่างเพื่อทำความเข้าใจกันดีกว่า ลองพิจารณาจำนวนผลไม้ที่เพื่อนบ้านของคุณมีในบ้านของพวกเขา
| เพื่อนบ้าน | จำนวนผลไม้ ( X) |
| แซม | 3 |
| ดาเนียล | 4 |
| โรบิน | 6 |
| แมรี่ | 7 |
| คิม | 9 |
จำนวนของผลไม้คือจุดข้อมูลที่แสดงโดย x และค่าเฉลี่ยจะแสดงด้วย \(\bar{x}\) ค่าเฉลี่ยสำหรับข้อมูลข้างต้นคือ
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
ตอนนี้สร้างตารางที่แสดงจุดข้อมูล( \(x\) ) ค่าเฉลี่ย ( \(\bar{x}\) ) และความแตกต่างของจุดข้อมูลจากค่าเฉลี่ย \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 น |
ค้นหาค่าเฉลี่ยของความแตกต่าง \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
ส่วนเบี่ยงเบนมาตรฐาน:
\(\sigma = \sqrt{4.56} = 2.13\)
ค่าเฉลี่ย = 5.8 ผลไม้
ส่วนเบี่ยงเบนมาตรฐาน = 2.13 ผลไม้
ตอนนี้เราสามารถหาได้ง่ายๆ ว่าใครอยู่ในค่าเบี่ยงเบนมาตรฐานหนึ่งค่าและใครอยู่นอกเหนือค่านี้ ค่าเบี่ยงเบนมาตรฐานช่วยให้เรารู้ว่ากรณีปกติและกรณีพิเศษคืออะไร
เราสามารถคาดว่าข้อมูลประมาณสองในสามจะอยู่ในช่วง +1 หรือ -1 ส่วนเบี่ยงเบนมาตรฐานจากค่าเฉลี่ย เราสามารถพูดได้ว่า \(\frac{2}{3}^{rd}\) ของเพื่อนบ้านมีผลไม้ในบ้านของพวกเขาระหว่าง 7.93(5.8 + 2.13) และ 3.67 (5.8 - 2.13)
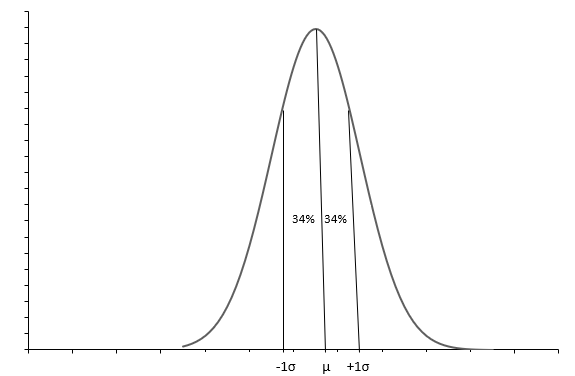
กราฟด้านบนแสดงการแจกแจงแบบปกติด้วยเส้นโค้งรูประฆัง การแจกแจงแบบปกติแต่ละรายการถูกกำหนดด้วยค่าเฉลี่ย( \(\mu\) ) และส่วนเบี่ยงเบนมาตรฐาน( \(\sigma\) ) ประมาณ 68% ของการสังเกตอยู่ระหว่าง \(+1\sigma\) และ \(-1\sigma\) ค่าเฉลี่ย( \(\mu\) ) ค่ามัธยฐานยังบอกเราถึงจุดกึ่งกลางของการแจกแจงซึ่งค่าข้อมูลทั้งหมดกระจายอยู่โดยรอบ ส่วนเบี่ยงเบนมาตรฐาน( \(\sigma\) ) บอกเราถึงวิธีการกระจายข้อมูล
ในการคำนวณส่วนเบี่ยงเบนมาตรฐานให้ทำตามขั้นตอนด้านล่าง:
1) หาค่าเฉลี่ย ( \(\bar{x}\) ) ของรายการข้อมูลในชุดที่กำหนด
2) นำผลต่างแต่ละรายการจากค่าเฉลี่ยมายกกำลังสองแล้วหาค่าเฉลี่ย ผลลัพธ์นี้เรียกว่าความแปรปรวน
3) หาค่ารากที่สองของความแปรปรวน ซึ่งจะให้ค่าเบี่ยงเบนมาตรฐาน \(\sigma\)