Ang ibig sabihin ng deviation ay kung gaano kalayo sa normal o average.
Magagamit natin ang standard deviation para malaman kung normal o kakaiba/pambihira ang ilang pag-uugali. Ang karaniwang paglihis ay kadalasang kinakalkula gamit ang mean ng isang set ng data, at nakakatulong ito sa amin na malaman kung paano nagkakalat ang data. Sa madaling salita, sa isang set ng data standard deviation ay nagsasabi sa amin kung gaano kahigpit ang lahat ng iba't ibang data point ay naka-cluster sa paligid ng mean. Ang standard deviation ay tinutukoy ng simbolo na \('\sigma'\) .
Ang standard deviation ay madaling kalkulahin gamit ang isang calculator, spreadsheet software o math formula na ipinaliwanag sa ibaba.
Kumuha tayo ng isang halimbawa upang mas maunawaan ito. Isaalang-alang natin ang bilang ng mga prutas na mayroon ang iyong mga kapitbahay sa kanilang mga bahay.
| Kapit-bahay | Bilang ng mga prutas ( X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Mary | 7 |
| Kim | 9 |
Ang bilang ng mga prutas ay mga punto ng data na tinutukoy ng x at ang Mean ay kinakatawan ng \(\bar{x}\) . Ang ibig sabihin para sa data sa itaas ay
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Bumuo ngayon ng talahanayan na nagpapakita ng mga data point( \(x\) ) , mean ( \(\bar{x}\) ) at pagkakaiba ng data point mula sa mean( \(x - \bar{x}\)
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Hanapin ang mean ng mga pagkakaiba \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Karaniwang lihis:
\(\sigma = \sqrt{4.56} = 2.13\)
Mean = 5.8 prutas
Standard Deviation = 2.13 prutas
Ngayon ay madali na nating malaman kung sino ang nasa loob ng isang standard deviation at kung sino ang lampas dito. Kaya tinutulungan tayo ng standard deviation na malaman kung ano ang mga normal na kaso at kung ano ang mga hindi pangkaraniwang kaso.
Maaari naming asahan ang humigit-kumulang dalawang-katlo ng data na mahuhulog sa loob ng +1 o -1 na karaniwang paglihis mula sa mean. Masasabi nating \(\frac{2}{3}^{rd}\) ng mga kapitbahay ay mayroong 7.93(5.8 + 2.13) at 3.67 (5.8 - 2.13) na prutas sa kanilang mga bahay.
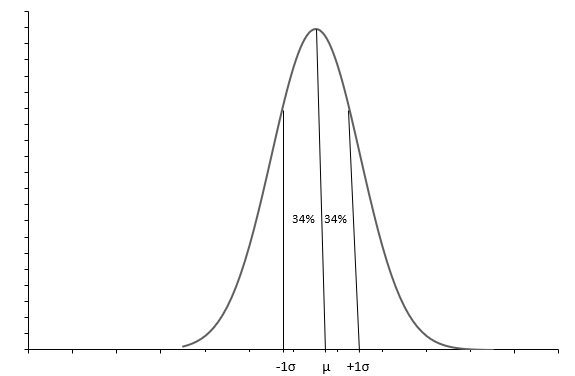
Ang graph sa itaas ay nagpapakita ng isang normal na distribusyon na may kurba ng hugis ng kampanilya. Ang bawat Normal na distribusyon ay tinutukoy ng mean( \(\mu\) ) at standard deviation( \(\sigma\) ). Tinatayang 68% ng mga obserbasyon ang nasa pagitan \(+1\sigma\) at \(-1\sigma\) . Ang mean( \(\mu\) ) din ang median ay nagsasabi sa atin ng mid-point ng distribution, kung saan ang lahat ng value ng data ay ikinakalat. Sinasabi sa atin ng standard deviation( \(\sigma\) ) kung paano ipagkalat ang data.
Upang kalkulahin ang standard deviation, sundin ang mga hakbang sa ibaba:
1) Maghanap ng mean( \(\bar{x}\) ) ng mga data item sa ibinigay na set
2) Kunin ang bawat pagkakaiba ng data item mula sa mean, parisukat ito, at pagkatapos ay i-average ang resulta. Ang resultang ito ay tinatawag na Variance
3) Kunin ang square root ng Variance, ito ay magbibigay ng Standard Deviation \(\sigma\)