Sapma, normalden veya ortalamadan ne kadar uzakta olduğu anlamına gelir.
Belirli bir davranışın normal mi yoksa benzersiz/olağanüstü mü olduğunu bilmek için standart sapmayı kullanabiliriz. Standart sapma genellikle bir veri setinin ortalaması ile hesaplanır ve verilerin ne kadar dağıldığını bilmemize yardımcı olur. Başka bir deyişle, bir veri kümesinde standart sapma, tüm çeşitli veri noktalarının ortalama etrafında ne kadar sıkı bir şekilde kümelendiğini söyler. Standart sapma \('\sigma'\) sembolü ile gösterilir.
Standart sapma, aşağıda açıklanan bir hesap makinesi, elektronik tablo yazılımı veya matematik formülleri kullanılarak kolayca hesaplanabilir.
Daha iyi anlamak için bir örnek verelim. Komşularınızın evlerinde bulunan meyve sayısını hesaplayalım.
| Komşu | meyve sayısı ( X) |
| Sam | 3 |
| Daniel | 4 |
| robin | 6 |
| Mary | 7 |
| Kim | 9 |
Meyve sayısı x ile gösterilen veri noktalarıdır ve Ortalama \(\bar{x}\) ile temsil edilir. Yukarıdaki veriler için ortalama
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Şimdi veri noktalarını( \(x\) ) , ortalamayı ( \(\bar{x}\) ) ve veri noktasının ortalamadan( \(x - \bar{x}\) ) farkını gösteren bir tablo oluşturun.
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Farkların ortalamasını bulun \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Standart sapma:
\(\sigma = \sqrt{4.56} = 2.13\)
Ortalama = 5.8 meyve
Standart Sapma = 2.13 meyve
Artık kimlerin bir standart sapma içinde ve kimin ötesinde olduğunu kolayca anlayabiliriz. Dolayısıyla standart sapma, neyin normal, neyin olağanüstü durum olduğunu bilmemize yardımcı olur.
Verilerin yaklaşık üçte ikisinin ortalamadan +1 veya -1 standart sapma içinde kalmasını bekleyebiliriz. Komşuların evlerinde 7,93(5,8 + 2,13) ile 3,67 (5,8 - 2,13) arasında \(\frac{2}{3}^{rd}\) ) meyve olduğunu söyleyebiliriz.
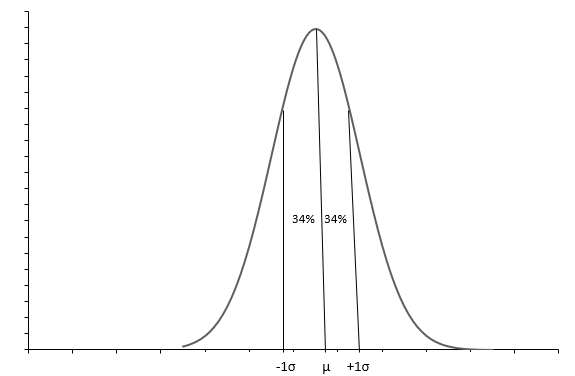
Yukarıdaki grafik, çan şeklindeki bir eğri ile normal bir dağılımı göstermektedir. Her Normal dağılım, ortalama ( \(\mu\) ) ve standart sapma ( \(\sigma\) ) ile tanımlanır. Gözlemlerin yaklaşık %68'i \(+1\sigma\) ve \(-1\sigma\) arasındadır. Ortalama( \(\mu\) ) aynı zamanda ortanca, bize tüm veri değerlerinin yayıldığı dağılımın orta noktasını söyler. Standart sapma( \(\sigma\) ) bize verilerin nasıl dağılacağını söyler.
Standart sapmayı hesaplamak için aşağıdaki adımları izleyin:
1) Verilen kümedeki veri öğelerinin ortalamasını ( \(\bar{x}\) ) bulun
2) Veri öğesinin her farkını ortalamadan alın, karesini alın ve ardından sonucun ortalamasını alın. Bu sonuca Varyans denir
3) Varyansın karekökünü alın, bu Standart Sapmayı verecek \(\sigma\)