Відхилення означає, наскільки далеко від нормального або середнього.
Ми можемо використовувати стандартне відхилення, щоб дізнатися, чи є певна поведінка нормальною чи унікальною/надзвичайною. Стандартне відхилення часто обчислюється за допомогою середнього значення набору даних, і це допомагає нам знати, наскільки розкидані дані. Іншими словами, у наборі даних стандартне відхилення говорить нам, наскільки тісно всі різні точки даних згруповані навколо середнього значення. Стандартне відхилення позначається символом \('\sigma'\) .
Стандартне відхилення можна легко обчислити за допомогою калькулятора, програмного забезпечення для роботи з електронними таблицями або математичних формул, які пояснюються нижче.
Візьмемо приклад, щоб краще зрозуміти. Давайте врахуємо кількість фруктів, які є у ваших сусідів.
| Сусідка | Кількість фруктів (X) |
| Сем | 3 |
| Даніель | 4 |
| Робін | 6 |
| Мері | 7 |
| Кім | 9 |
Кількість фруктів – це точки даних, які позначаються x, а середнє значення представлене \(\bar{x}\) . Середнє для наведених вище даних становить
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Тепер сформуйте таблицю, яка показує точки даних ( \(x\) ), середнє ( \(\bar{x}\) і різницю точки даних від середнього ( \(x - \bar{x}\)
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7,84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Знайдіть середнє значення різниць \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Стандартне відхилення:
\(\sigma = \sqrt{4.56} = 2.13\)
Середнє = 5,8 плодів
Стандартне відхилення = 2,13 плодів
Тепер ми можемо легко визначити, хто знаходиться в межах одного стандартного відхилення, а хто за його межами. Таким чином, стандартне відхилення допомагає нам знати, що є нормальними випадками, а які — надзвичайними.
Ми можемо очікувати, що приблизно дві третини даних потраплятимуть у межах +1 або -1 стандартного відхилення від середнього. Ми можемо сказати \(\frac{2}{3}^{rd}\) сусідів мають у своїх будинках від 7,93(5,8 + 2,13) до 3,67 (5,8 - 2,13) фруктів.
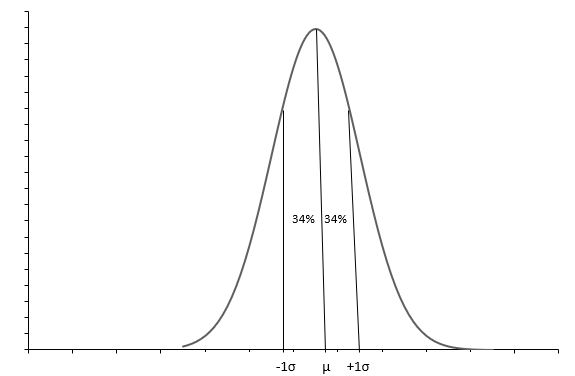
Наведений вище графік показує нормальний розподіл із дзвоноподібною кривою. Кожен нормальний розподіл визначається середнім ( \(\mu\) ) і стандартним відхиленням ( \(\sigma\) ). Приблизно 68% спостережень знаходяться між \(+1\sigma\) і \(-1\sigma\) . Середнє значення ( \(\mu\) ) також медіана вказує нам середину розподілу, навколо якої розподіляються всі значення даних. Стандартне відхилення ( \(\sigma\) ) говорить нам, як розподілити дані.
Щоб обчислити стандартне відхилення, виконайте наведені нижче дії.
1) Знайти середнє ( \(\bar{x}\) ) елементів даних у заданому наборі
2) Візьміть кожну різницю елементів даних із середнього, зведіть його в квадрат, а потім усередніть результат. Цей результат називається дисперсією
3) Візьміть квадратний корінь із дисперсії, це дасть стандартне відхилення \(\sigma\)