انحراف کا مطلب ہے کہ عام یا اوسط سے کتنا دور ہے۔
ہم معیاری انحراف کا استعمال یہ جاننے کے لیے کر سکتے ہیں کہ آیا کچھ طرز عمل نارمل ہے یا منفرد/غیر معمولی۔ معیاری انحراف کا شمار اکثر ڈیٹا سیٹ کے وسط سے کیا جاتا ہے، اور اس سے ہمیں یہ جاننے میں مدد ملتی ہے کہ ڈیٹا کتنا پھیلا ہوا ہے۔ دوسرے الفاظ میں، ڈیٹا کے ایک سیٹ میں معیاری انحراف ہمیں بتاتا ہے کہ تمام مختلف ڈیٹا پوائنٹس کو وسط کے گرد کس قدر مضبوطی سے کلسٹر کیا گیا ہے۔ معیاری انحراف کو علامت \('\sigma'\) سے ظاہر کیا جاتا ہے۔
معیاری انحراف کا حساب آسانی سے ایک کیلکولیٹر، اسپریڈشیٹ سافٹ ویئر یا ریاضی کے فارمولوں کے ذریعے لگایا جا سکتا ہے جن کی ذیل میں وضاحت کی گئی ہے۔
آئیے اسے بہتر طور پر سمجھنے کے لیے ایک مثال لیتے ہیں۔ آئیے آپ کے پڑوسیوں کے گھروں میں کتنے پھل ہیں۔
| پڑوسی | پھلوں کی تعداد (X) |
| سام | 3 |
| دانیال | 4 |
| رابن | 6 |
| مریم | 7 |
| کم | 9 |
پھلوں کی تعداد ڈیٹا پوائنٹس ہیں جن کو x سے ظاہر کیا جاتا ہے اور Mean کو \(\bar{x}\) سے ظاہر کیا جاتا ہے۔ مندرجہ بالا اعداد و شمار کا مطلب ہے
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
اب ایک ٹیبل بنائیں جو ڈیٹا پوائنٹس ( \(x\) ) , مطلب ( \(\bar{x}\) ) اور ڈیٹا پوائنٹ کے وسط سے فرق دکھاتا ہے( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0.04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
فرق کا اوسط تلاش کریں \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
معیاری انحراف:
\(\sigma = \sqrt{4.56} = 2.13\)
اوسط = 5.8 پھل
معیاری انحراف = 2.13 پھل
اب ہم آسانی سے اندازہ لگا سکتے ہیں کہ ایک معیاری انحراف میں کون ہیں اور کون اس سے باہر ہیں۔ لہذا معیاری انحراف سے ہمیں یہ جاننے میں مدد ملتی ہے کہ نارمل کیسز کیا ہیں اور غیر معمولی کیسز کیا ہیں۔
ہم توقع کر سکتے ہیں کہ تقریباً دو تہائی ڈیٹا اوسط سے +1 یا -1 معیاری انحراف کے اندر آئے گا۔ ہم کہہ سکتے ہیں کہ پڑوسیوں کے \(\frac{2}{3}^{rd}\) کے گھروں میں 7.93 (5.8 + 2.13) اور 3.67 (5.8 - 2.13) کے درمیان پھل ہیں۔
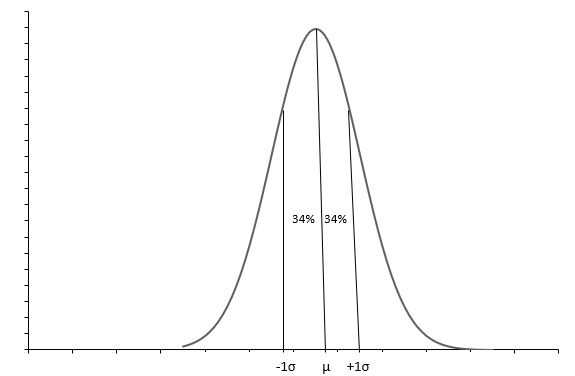
اوپر والا گراف گھنٹی کی شکل کے وکر کے ساتھ ایک عام تقسیم کو ظاہر کرتا ہے۔ ہر عام تقسیم کی وضاحت وسط( \(\mu\) ) اور معیاری انحراف ( \(\sigma\) ) کے ساتھ کی جاتی ہے۔ تقریباً 68% مشاہدات \(+1\sigma\) اور \(-1\sigma\) کے درمیان آتے ہیں۔ اوسط ( \(\mu\) ) بھی میڈین ہمیں تقسیم کا وسط نقطہ بتاتا ہے، جس کے ارد گرد تمام ڈیٹا ویلیوز پھیلی ہوئی ہیں۔ معیاری انحراف ( \(\sigma\) ) ہمیں بتاتا ہے کہ ڈیٹا کو کیسے پھیلایا جائے۔
معیاری انحراف کا حساب لگانے کے لیے درج ذیل مراحل پر عمل کریں:
1) دیے گئے سیٹ میں ڈیٹا آئٹمز کا مطلب ( \(\bar{x}\) ) تلاش کریں۔
2) ڈیٹا آئٹم کے ہر فرق کو وسط سے لیں، اس کا مربع کریں، اور پھر نتیجہ کا اوسط نکالیں۔ اس نتیجہ کو Variance کہا جاتا ہے۔
3) تغیر کا مربع جڑ لیں، یہ معیاری انحراف دے گا \(\sigma\)