Og'ish normadan yoki o'rtachadan qanchalik uzoq ekanligini anglatadi.
Muayyan xatti-harakatlar normal yoki noyob/g'ayrioddiy ekanligini bilish uchun standart og'ishdan foydalanishimiz mumkin. Standart og'ish ko'pincha ma'lumotlar to'plamining o'rtacha qiymati bilan hisoblanadi va bu bizga ma'lumotlar qanchalik tarqalishini bilishga yordam beradi. Boshqacha qilib aytganda, ma'lumotlar to'plamida standart og'ish barcha turli xil ma'lumotlar nuqtalarining o'rtacha atrofida qanchalik zich joylashganligini ko'rsatadi. Standart og'ish \('\sigma'\) belgisi bilan belgilanadi.
Standart og'ish kalkulyator, elektron jadval dasturi yoki quyida tushuntirilgan matematik formulalar yordamida osongina hisoblanishi mumkin.
Buni yaxshiroq tushunish uchun bir misol keltiraylik. Keling, qo'shnilaringizning uylarida qancha mevalar borligini hisobga olaylik.
| Qo'shni | Mevalar soni (X) |
| Sam | 3 |
| Daniel | 4 |
| Robin | 6 |
| Meri | 7 |
| Kim | 9 |
Mevalar soni ma'lumotlar nuqtalari bo'lib, ular x bilan belgilanadi, o'rtacha esa \(\bar{x}\) bilan ifodalanadi. Yuqoridagi ma'lumotlar uchun o'rtacha
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Endi ma'lumotlar nuqtalari ( \(x\) ) , o'rtacha ( \(\bar{x}\) ) va ma'lumotlar nuqtasining o'rtacha ( \(x - \bar{x}\) ) farqini ko'rsatadigan jadval tuzing.
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5.8 | 7.84 |
| 4 | 5.8 | 3.24 |
| 6 | 5.8 | 0,04 |
| 7 | 5.8 | 1.44 |
| 9 | 5.8 | 10.24 |
Farqlarning oʻrtacha qiymatini toping \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Standart og'ish:
\(\sigma = \sqrt{4.56} = 2.13\)
O'rtacha = 5,8 meva
Standart og'ish = 2,13 meva
Endi biz bitta standart og'ish doirasida kim va undan tashqarida ekanligini osongina aniqlashimiz mumkin. Shunday qilib, standart og'ish bizga oddiy holatlar nima va favqulodda holatlar nima ekanligini bilishga yordam beradi.
Biz ma'lumotlarning uchdan ikki qismi o'rtacha qiymatdan +1 yoki -1 standart og'ish chegarasiga tushishini kutishimiz mumkin. Aytishimiz mumkinki, qo'shnilarning \(\frac{2}{3}^{rd}\) uylarida 7,93(5,8 + 2,13) va 3,67 (5,8 - 2,13) gacha meva bor.
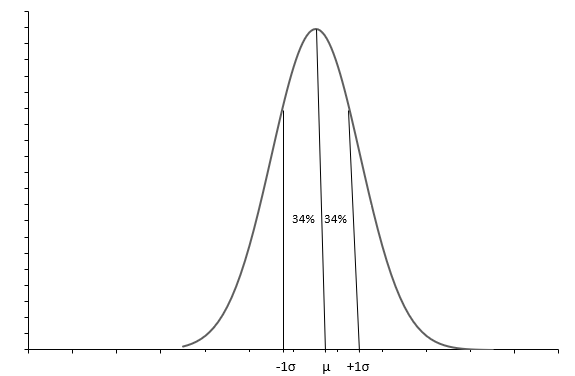
Yuqoridagi grafikda qo'ng'iroq shakli egri chizig'i bilan normal taqsimot ko'rsatilgan. Har bir Oddiy taqsimot o'rtacha ( \(\mu\) ) va standart og'ish ( \(\sigma\) ) bilan aniqlanadi. Kuzatishlarning taxminan 68% \(+1\sigma\) va \(-1\sigma\) oralig'iga to'g'ri keladi. O'rtacha ( \(\mu\) ) shuningdek, median bizga taqsimotning o'rta nuqtasini bildiradi, uning atrofida barcha ma'lumotlar qiymatlari tarqaladi. Standart og'ish ( \(\sigma\) ) bizga ma'lumotlarni qanday tarqatish kerakligini aytadi.
Standart og'ishlarni hisoblash uchun quyidagi amallarni bajaring:
1) Berilgan toʻplamdagi maʼlumotlar elementlarining oʻrtacha( \(\bar{x}\) qiymatini toping
2) Ma'lumotlar elementining har bir farqini o'rtacha qiymatdan oling, kvadratga oling va natijani o'rtachalang. Bu natija Variant deb ataladi
3) Variantning kvadrat ildizini oling, bu standart og'ish \(\sigma\) ni beradi.