Độ lệch có nghĩa là bao xa so với mức bình thường hoặc trung bình.
Chúng ta có thể sử dụng độ lệch chuẩn để biết liệu hành vi nào đó là bình thường hay độc đáo/bất thường. Độ lệch chuẩn thường được tính toán với giá trị trung bình của một tập dữ liệu và nó giúp chúng tôi biết mức độ lan truyền của dữ liệu. Nói cách khác, trong một tập hợp dữ liệu, độ lệch chuẩn cho chúng ta biết mức độ chặt chẽ của tất cả các điểm dữ liệu khác nhau được nhóm xung quanh giá trị trung bình. Độ lệch chuẩn được biểu thị bằng ký hiệu \('\sigma'\) .
Có thể dễ dàng tính toán độ lệch chuẩn bằng máy tính, phần mềm bảng tính hoặc công thức toán học được giải thích bên dưới.
Hãy lấy một ví dụ để hiểu rõ hơn. Hãy đếm số lượng trái cây mà hàng xóm của bạn có trong nhà của họ.
| Láng giềng | Số quả (X) |
| Sâm | 3 |
| Đa-ni-ên | 4 |
| robin | 6 |
| ma-ri-a | 7 |
| Kim | 9 |
Số lượng trái cây là các điểm dữ liệu được biểu thị bằng x và Giá trị trung bình được biểu thị bằng \(\bar{x}\) . Có nghĩa là cho các dữ liệu trên là
\(\bar{x} = \frac{3+4+6+7+9}{5} = 5.8\)
Bây giờ hãy tạo một bảng hiển thị các điểm dữ liệu ( \(x\) ) , giá trị trung bình ( \(\bar{x}\) ) và sự khác biệt của điểm dữ liệu so với giá trị trung bình ( \(x - \bar{x}\) )
| \(x\) | \(\bar{x}\) | \((x - \bar{x})^2\) |
| 3 | 5,8 | 7,84 |
| 4 | 5,8 | 3,24 |
| 6 | 5,8 | 0,04 |
| 7 | 5,8 | 1,44 |
| 9 | 5,8 | 10.24 |
Tìm giá trị trung bình của các chênh lệch \(= \frac{7.84+3.24+.04+1.44+10.24}{5} = 4.56\)
Độ lệch chuẩn:
\(\sigma = \sqrt{4.56} = 2.13\)
Có nghĩa là = 5,8 quả
Độ lệch chuẩn = 2,13 quả
Bây giờ chúng ta có thể dễ dàng tìm ra ai nằm trong một độ lệch chuẩn và ai vượt quá nó. Vì vậy, độ lệch chuẩn giúp chúng ta biết đâu là trường hợp bình thường và đâu là trường hợp bất thường.
Chúng ta có thể mong đợi khoảng hai phần ba dữ liệu nằm trong độ lệch chuẩn +1 hoặc -1 so với giá trị trung bình. Có thể nói \(\frac{2}{3}^{rd}\) hàng xóm có từ 7,93(5,8 + 2,13) đến 3,67 (5,8 - 2,13) trái cây trong nhà của họ.
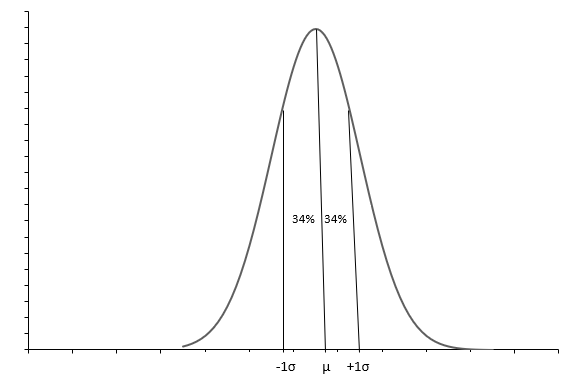
Biểu đồ trên cho thấy một phân phối bình thường với một đường cong hình chuông. Mỗi phân phối Chuẩn được xác định bằng giá trị trung bình ( \(\mu\) ) và độ lệch chuẩn ( \(\sigma\) ). Khoảng 68% quan sát nằm trong khoảng \(+1\sigma\) và \(-1\sigma\) . Giá trị trung bình ( \(\mu\) ) cũng là trung vị cho chúng ta biết điểm giữa của phân phối, xung quanh đó tất cả các giá trị dữ liệu được trải đều. Độ lệch chuẩn ( \(\sigma\) ) cho chúng ta biết dữ liệu được trải ra như thế nào.
Để tính độ lệch chuẩn, hãy làm theo các bước sau:
1) Tìm giá trị trung bình ( \(\bar{x}\) ) của các mục dữ liệu trong tập hợp đã cho
2) Lấy mỗi chênh lệch của mục dữ liệu từ giá trị trung bình, bình phương giá trị đó và sau đó tính trung bình kết quả. Kết quả này được gọi là Phương sai
3) Lấy căn bậc hai của Phương sai, điều này sẽ cho Độ lệch chuẩn \(\sigma\)