Back to the topics list

إحداثيات قطبية

الإحداثيات القطبية هي طريقة لتمثيل نقطة في الفضاء.

أ- القطب

ب- المحور القطبي

ص- تنسيق شعاعي

θ - تنسيق الزاوي

يشير نظام الإحداثيات القطبية إلى نظام إحداثيات ثنائي الأبعاد تتأثر فيه كل نقطة على مستوى بمسافة من نقطة مرجعية وزاوية من اتجاه مرجعي. إذن ، في الإحداثيات القطبية ، نتحدث عن مسافة النقطة من القطب A الممثلة هنا بالرمز r ، والزاوية التي تصنعها مع المحور للوصول إلى النقطة D وهي θ هنا.

يشار إلى النقطة المرجعية (التي تشبه أصل نظام الإحداثيات الديكارتية) بالقطب . الشعاع القادم من القطب في اتجاه المرجع هو ما يعرف بالمحور القطبي . نصف القطر أو المسافة الشعاعية أو الإحداثيات الشعاعية هي المسافة من القطب. يشار إلى الزاوية من القطب باسم السمت أو الزاوية القطبية أو الإحداثي الزاوي.

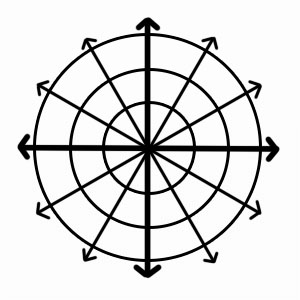
لتحديد نقطة في الإحداثيات القطبية ، نستخدم الترميز (r ، θ) ، حيث r هي المسافة من الأصل إلى النقطة ، و هي الزاوية المقاسة عكس اتجاه عقارب الساعة من المحور القطبي إلى الخط الذي يربط الأصل بالنقطة .

للتحويل بين الإحداثيات القطبية والمستطيلة (النظام التقليدي (x ، y)) ، نستخدم الصيغ التالية:

\(x = r \times \cosθ\)

\(y = r \times \sinθ\)

على العكس من ذلك ، للتحويل من إحداثيات مستطيلة إلى إحداثيات قطبية ، نستخدم الصيغ:

\(r = \sqrt{x^2 + y^2}\)

\(θ = \tan^{-1}{\frac{y}{x}}\)

هنا، تان ^-1 هي دالة تأخذ وسيطين (y و x) وتعيد الزاوية بين المحور x الموجب والخط الذي يمر عبر الأصل و (x ، y) ، تقاس عكس اتجاه عقارب الساعة.

الإحداثيات القطبية مفيدة بشكل خاص في المواقف التي تتضمن تناظرًا دائريًا أو دورانيًا ، مثل وصف مواضع النقاط على عجلة أو حركة البندول. كما أنها تستخدم على نطاق واسع في الفيزياء والهندسة لوصف حركة الأجسام في الإحداثيات القطبية ، مثل الأقمار الصناعية التي تدور حول الأرض.

التحويل

لتحويل إحداثي من إحداثيات قطبية إلى إحداثيات ديكارتية أو العكس ، نستخدم مثلثًا.

التحويل من كارتيزي إلى قطبي

في حال عرفنا نقطة في الإحداثيات الديكارتية (س ، ص) وأردنا تحويلها إلى إحداثيات قطبية (ص ،) ، نبدأ بحل مثلث قائم الزاوية مع ضلعين معروفين.

على سبيل المثال ، ما هو (12 ، 5) في الإحداثيات القطبية؟

حل

استخدم نظرية فيثاغورس لإيجاد الضلع الطويل (وتر المثلث).

ص ² = 12 ² + 5 ²

ص ² = 169

ص = 13

الخطوة الثانية هي استخدام دالة الظل لإيجاد الزاوية ،

\(\tanθ = {5 \over 12}\)

\(θ = \tan^{-1} {\frac{5}{12}} = 22.6⁰ \) (حتى علامة عشرية واحدة).

الإجابة: النقطة (12.5) هي (13 ، 22.6 درجة) في الإحداثيات القطبية.

التحويل من القطبية إلى الكارتيزية

في حالة معرفتنا نقطة في الإحداثيات القطبية (ص ، θ) ، ونرغب في تحويلها إلى إحداثيات ديكارتية (س ، ص) ، فإننا نحل مثلث قائم الزاوية بوتر وزاوية معروفين.

على سبيل المثال: قم بتحويل (13 ، 22.6 درجة) إلى الإحداثيات الديكارتية.

حل

استخدم دالة جيب التمام لـ x: \(\cos 22.6⁰ = \frac{x}{13}\)

س = \(13 \times \cos 22.6⁰\)

س = 13 × 0.923

س = 12.002

س = 12 (تقريب)

استخدم دالة الجيب لـ y: \(\sin 22.6⁰ = \frac{y}{13}\)

ص = 13 × \(\sin 22.6⁰\)

ص = 13 × 0.391

ص = 4.996

ص = 5 (تقريب)

الإجابة: النقطة (13 ، 22.6 درجة) هي (12 ، 5) في الإحداثيات الديكارتية.