ध्रुवीय निर्देशांक अंतरिक्ष में एक बिंदु का प्रतिनिधित्व करने का एक तरीका है।
एक खंभा
बी- ध्रुवीय अक्ष
आर- रेडियल समन्वय
θ - कोणीय समन्वय
एक ध्रुवीय समन्वय प्रणाली एक द्वि-आयामी समन्वय प्रणाली को संदर्भित करती है जिसमें एक विमान पर प्रत्येक बिंदु संदर्भ बिंदु से दूरी और संदर्भ की दिशा से कोण से प्रभावित होता है। तो ध्रुवीय निर्देशांक में, हम ध्रुव A से बिंदु की दूरी के बारे में बात करते हैं जिसे यहाँ r के रूप में दर्शाया गया है, और वह कोण जो अक्ष के साथ बिंदु D तक पहुँचने के लिए बनाता है जो यहाँ θ है।
संदर्भ बिंदु (जो कार्टेशियन समन्वय प्रणाली की उत्पत्ति के समान है) को ध्रुव कहा जाता है। संदर्भ की दिशा में ध्रुव से आने वाली किरण को ध्रुवीय अक्ष के रूप में जाना जाता है। रेडियस, रेडियल दूरी या रेडियल कोऑर्डिनेट ध्रुव से दूरी है। ध्रुव से कोण को दिगंश , ध्रुवीय कोण या कोणीय निर्देशांक कहा जाता है।
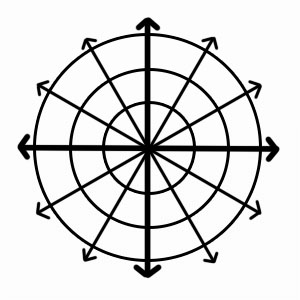
ध्रुवीय निर्देशांक में एक बिंदु को परिभाषित करने के लिए, हम अंकन (r, θ) का उपयोग करते हैं, जहां r मूल से बिंदु तक की दूरी है, और θ वह कोण है जिसे ध्रुवीय अक्ष से वामावर्त मापा जाता है, जो मूल बिंदु को बिंदु से जोड़ता है। .
ध्रुवीय और आयताकार निर्देशांक (पारंपरिक (x, y) प्रणाली) के बीच परिवर्तित करने के लिए, हम निम्नलिखित सूत्रों का उपयोग करते हैं:
\(x = r \times \cosθ\)
\(y = r \times \sinθ\)
इसके विपरीत, आयताकार निर्देशांकों को ध्रुवीय निर्देशांकों में बदलने के लिए, हम सूत्रों का उपयोग करते हैं:
\(r = \sqrt{x^2 + y^2}\)
\(θ = \tan^{-1}{\frac{y}{x}}\)
यहाँ,
ध्रुवीय निर्देशांक विशेष रूप से उन स्थितियों में उपयोगी होते हैं जिनमें वृत्ताकार या घूर्णी समरूपता शामिल होती है, जैसे कि एक पहिया पर बिंदुओं की स्थिति का वर्णन करना या एक पेंडुलम की गति। वे ध्रुवीय निर्देशांक में वस्तुओं की गति का वर्णन करने के लिए भौतिक विज्ञान और इंजीनियरिंग में भी बड़े पैमाने पर उपयोग किए जाते हैं, जैसे उपग्रह पृथ्वी की परिक्रमा करते हैं।
परिवर्तित
एक को ध्रुवीय निर्देशांक से कार्तीय निर्देशांक में बदलने के लिए या इसके विपरीत, हम एक त्रिकोण का उपयोग करते हैं।
कार्तीय से ध्रुवीय में परिवर्तन
यदि हम कार्तीय निर्देशांक (x, y) में एक बिंदु जानते हैं और हम इसे ध्रुवीय निर्देशांक (r, θ) में परिवर्तित करना चाहते हैं, तो हम ज्ञात दो भुजाओं वाले एक समकोण त्रिभुज को हल करके प्रारंभ करते हैं।
उदाहरण के लिए, ध्रुवीय निर्देशांकों में (12, 5) क्या है?
समाधान
लंबी भुजा (कर्ण) ज्ञात करने के लिए पाइथागोरस प्रमेय का उपयोग करें।
आर 2 = 12 2 + 5 2
आर 2 = 169
आर = 13
दूसरा चरण कोण खोजने के लिए स्पर्शरेखा फ़ंक्शन का उपयोग करना है,
\(\tanθ = {5 \over 12}\)
\(θ = \tan^{-1} {\frac{5}{12}} = 22.6⁰ \) (एक दशमलव बिंदु तक)।
उत्तर: बिंदु (12,5) ध्रुवीय निर्देशांक में (13, 22.6°) है।
ध्रुवीय से कार्तीय में परिवर्तन
यदि हम ध्रुवीय निर्देशांक (r, θ) में एक बिंदु जानते हैं, और हम इसे कार्तीय निर्देशांक (x, y) में बदलना चाहते हैं, तो हम एक ज्ञात कर्ण और कोण के साथ एक समकोण त्रिभुज को हल करते हैं।
उदाहरण के लिए: (13, 22.6°) को कार्तीय निर्देशांक में बदलें।
समाधान
x के लिए कोज्या फलन का प्रयोग करें: \(\cos 22.6⁰ = \frac{x}{13}\)
x = \(13 \times \cos 22.6⁰\)
एक्स = 13 × 0.923
एक्स = 12.002
x = 12 (राउंड ऑफ)
y के लिए ज्या फलन का प्रयोग करें: \(\sin 22.6⁰ = \frac{y}{13}\)
y = 13 × \(\sin 22.6⁰\)
वाई = 13 × 0.391
वाई = 4.996
y = 5 (राउंड ऑफ)
उत्तर: बिंदु (13, 22.6°) कार्तीय निर्देशांक में (12, 5) है।