Back to the topics list

polarne koordinate

Polarna koordinata je način predstavljanja točke u prostoru.

Stup

B- Polarna os

r- Radijalna koordinata

θ - kutna koordinata

Polarni koordinatni sustav odnosi se na dvodimenzionalni koordinatni sustav u kojem je svaka točka na ravnini pod utjecajem udaljenosti od referentne točke i kuta od referentnog smjera. Dakle, u polarnim koordinatama, govorimo o udaljenosti točke od pola A koja je ovdje predstavljena kao r, i kutu koji ona čini s osi do točke D koja je ovdje θ.

Referentna točka (koja je analogna ishodištu kartezijevog koordinatnog sustava) naziva se pol . Zraka od pola u referentnom smjeru je ono što je poznato kao polarna os . Radijus, radijalna udaljenost ili radijalna koordinata je udaljenost od pola. Kut od pola naziva se azimut , polarni kut ili kutna koordinata.

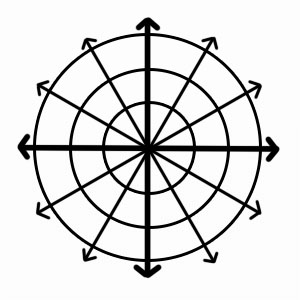
Za definiranje točke u polarnim koordinatama koristimo oznaku (r, θ), gdje je r udaljenost od ishodišta do točke, a θ je kut mjeren u smjeru suprotnom od kazaljke na satu od polarne osi do crte koja povezuje ishodište s točkom .

Za pretvorbu između polarnih i pravokutnih koordinata (tradicionalni (x, y) sustav), koristimo sljedeće formule:

\(x = r \times \cosθ\)

\(y = r \times \sinθ\)

Obrnuto, za pretvorbu pravokutnih koordinata u polarne koordinate koristimo formule:

\(r = \sqrt{x^2 + y^2}\)

\(θ = \tan^{-1}{\frac{y}{x}}\)

Ovdje, preplanulost ^-1 je funkcija koja uzima dva argumenta (y i x) i vraća kut između pozitivne x-osi i linije koja prolazi kroz ishodište i (x, y), mjeren u smjeru suprotnom od kazaljke na satu.

Polarne koordinate posebno su korisne u situacijama koje uključuju kružnu ili rotacijsku simetriju, kao što je opisivanje položaja točaka na kotaču ili kretanja njihala. Također se intenzivno koriste u fizici i inženjerstvu za opisivanje gibanja objekata u polarnim koordinatama, poput satelita koji kruže oko Zemlje.

PRETVARANJE

Za pretvorbu polarne koordinate u kartezijevu koordinatu ili obrnuto koristimo trokut.

PRELAZAK IZ KARTEZIJANSKOG U POLARNI

U slučaju da znamo točku u Kartezijevim koordinatama (x, y) i želimo je pretvoriti u polarne koordinate (r, θ), počinjemo rješavanjem pravokutnog trokuta s dvije poznate stranice.

Na primjer, Što je (12, 5) u polarnim koordinatama?

RIJEŠENJE

Upotrijebite Pitagorin teorem da pronađete dužu stranicu (hipotenuzu).

r ² = 12 ² + 5 ²

r ² = 169

r = 13

Drugi korak je korištenje funkcije tangensa za pronalaženje kuta,

\(\tanθ = {5 \over 12}\)

\(θ = \tan^{-1} {\frac{5}{12}} = 22.6⁰ \) (na jednu decimalnu točku).

Odgovor: Točka (12,5) je (13, 22,6°) u polarnim koordinatama.

PRELAZAK IZ POLARNOG U KARTEZIJAN

U slučaju da znamo točku u polarnim koordinatama (r, θ), a želimo je pretvoriti u kartezijeve koordinate (x,y), rješavamo pravokutni trokut s poznatom hipotenuzom i kutom.

Na primjer: pretvorite (13, 22,6°) u Kartezijeve koordinate.

RIJEŠENJE

Koristite kosinusnu funkciju za x: \(\cos 22.6⁰ = \frac{x}{13}\)

x = \(13 \times \cos 22.6⁰\)

x = 13 × 0,923

x = 12,002

x = 12 (zaokružiti)

Upotrijebite funkciju sinusa za y: \(\sin 22.6⁰ = \frac{y}{13}\)

y = 13 × \(\sin 22.6⁰\)

y = 13 × 0,391

y = 4,996

y = 5 (zaokruži)

Odgovor: Točka (13, 22,6°) je (12, 5) u Kartezijevim koordinatama.