Back to the topics list

поларни координати

Поларната координата е начин да се претстави точка во просторот.

А- Пол

Б- Поларна оска

r- Радијална координата

θ - Аголна координата

Поларен координатен систем се однесува на дводимензионален координатен систем во кој секоја точка на рамнината е под влијание на растојание од референтна точка и агол од референтна насока. Значи, во поларните координати, зборуваме за растојанието на точката од полот A што овде е претставена како r, и аголот што таа го прави со оската за да достигне до точката D што е θ овде.

Референтната точка (која е аналогна на потеклото на Декартов координатен систем) се нарекува пол . Зракот од полот во референтната насока е она што е познато како поларна оска . Радиус, радијално растојание или радијална координата е растојанието од полот. Аголот од полот се нарекува азимут , поларен агол или аголна координата.

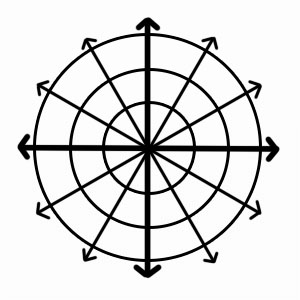
За да дефинираме точка во поларните координати, ја користиме ознаката (r, θ), каде што r е растојанието од потеклото до точката, а θ е аголот измерен спротивно од стрелките на часовникот од поларната оска до линијата што го поврзува потеклото со точката. .

За конвертирање помеѓу поларни и правоаголни координати (традиционалниот (x, y) систем), ги користиме следните формули:

\(x = r \times \cosθ\)

\(y = r \times \sinθ\)

Спротивно на тоа, за претворање од правоаголни координати во поларни координати, ги користиме формулите:

\(r = \sqrt{x^2 + y^2}\)

\(θ = \tan^{-1}{\frac{y}{x}}\)

Еве, тен ^-1 е функција која зема два аргументи (y и x) и го враќа аголот помеѓу позитивната оска x и правата што минува низ почетокот и (x, y), измерена спротивно од стрелките на часовникот.

Поларните координати се особено корисни во ситуации кои вклучуваат кружна или ротациона симетрија, како што е опишување на позициите на точките на тркалото или движењето на нишалото. Тие исто така се користат многу во физиката и инженерството за да се опише движењето на објектите во поларните координати, како што се сателитите кои орбитираат околу земјата.

КОНВЕРТИРАЊЕ

За да конвертираме една од поларна координата во Декарова координата или обратно, користиме триаголник.

КОНВЕРТИРАЊЕ ОД КАРТЕЗИЈАН НА ПОЛАРЕН

Во случај да знаеме точка во Декартови координати (x, y) и сакаме да ја претвориме во поларни координати (r, θ), започнуваме со решавање правоаголен триаголник со две познати страни.

На пример, Што е (12, 5) во поларните координати?

РЕШЕНИЕ

Користете ја теоремата на Питагора за да ја пронајдете долгата страна (хипотенуза).

r ² = 12 ² + 5 ²

r ² = 169

r = 13

Вториот чекор е да се користи функцијата тангента за да се најде аголот,

\(\tanθ = {5 \over 12}\)

\(θ = \tan^{-1} {\frac{5}{12}} = 22.6⁰ \) (до една децимална точка).

Одговор: Точката (12,5) е (13, 22,6°) во поларните координати.

КОНВЕРТИРАЊЕ ОД ПОЛАРНО ВО ДЕКАРСКО

Во случај да знаеме точка во поларни координати (r, θ), и сакаме да ја претвориме во Декартови координати (x,y), решаваме правоаголен триаголник со позната хипотенуза и агол.

На пример: претворете (13, 22,6°) во Декартови координати.

РЕШЕНИЕ

Користете ја функцијата косинус за x: \(\cos 22.6⁰ = \frac{x}{13}\)

x = \(13 \times \cos 22.6⁰\)

x = 13 × 0,923

x = 12.002

x = 12 (заокружување)

Користете ја синусната функција за y: \(\sin 22.6⁰ = \frac{y}{13}\)

y = 13 × \(\sin 22.6⁰\)

y = 13 × 0,391

y = 4,996

y = 5 (заокружување)

Одговор: Точката (13, 22,6°) е (12, 5) во Декартови координати.