Back to the topics list

полярные координаты

Полярная координата — это способ представления точки в пространстве.

А- Полюс

B- полярная ось

r- Радиальная координата

θ - угловая координата

Полярная система координат относится к двумерной системе координат, в которой на каждую точку плоскости влияет расстояние от точки отсчета и угол от направления отсчета. Таким образом, в полярных координатах мы говорим о расстоянии точки от полюса A, которое представлено здесь как r, и угле, который она образует с осью, чтобы достичь точки D, которая здесь равна θ.

Исходная точка (которая аналогична началу декартовой системы координат) называется полюсом . Луч от полюса в направлении отсчета известен как полярная ось . Радиус, радиальное расстояние или радиальная координата — это расстояние от полюса. Угол от полюса называется азимутом , полярным углом или угловой координатой.

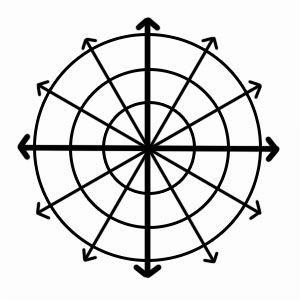
Для определения точки в полярных координатах мы используем обозначение (r, θ), где r — расстояние от начала координат до точки, а θ — угол, измеряемый против часовой стрелки от полярной оси до линии, соединяющей начало координат с точкой .

Для преобразования между полярными и прямоугольными координатами (традиционная система (x, y)) мы используем следующие формулы:

\(x = r \times \cosθ\)

\(y = r \times \sinθ\)

И наоборот, чтобы преобразовать прямоугольные координаты в полярные координаты, мы используем формулы:

\(r = \sqrt{x^2 + y^2}\)

\(θ = \tan^{-1}{\frac{y}{x}}\)

Здесь, загар ^-1 это функция, которая принимает два аргумента (y и x) и возвращает угол между положительной осью x и линией, проходящей через начало координат и (x, y), измеренный против часовой стрелки.

Полярные координаты особенно полезны в ситуациях, связанных с круговой или вращательной симметрией, например, для описания положения точек на колесе или движения маятника. Они также широко используются в физике и технике для описания движения объектов в полярных координатах, таких как спутники, вращающиеся вокруг Земли.

ПРЕОБРАЗОВАНИЕ

Чтобы преобразовать одну из полярных координат в декартовы координаты или наоборот, мы используем треугольник.

ПРЕОБРАЗОВАНИЕ ИЗ ДЕКРАТОВЫХ К ПОЛЯРНЫМ

Если мы знаем точку в декартовых координатах (x, y) и хотим преобразовать ее в полярные координаты (r, θ), мы начинаем с решения прямоугольного треугольника с двумя известными сторонами.

Например, что такое (12, 5) в полярных координатах?

РЕШЕНИЕ

Используйте теорему Пифагора, чтобы найти длинную сторону (гипотенузу).

г ² = 12 ² + 5 ²

г ² = 169

р = 13

Второй шаг - использовать функцию тангенса, чтобы найти угол,

\(\tanθ = {5 \over 12}\)

\(θ = \tan^{-1} {\frac{5}{12}} = 22.6⁰ \) (с точностью до одной десятичной точки).

Ответ: Точка (12,5) равна (13, 22,6°) в полярных координатах.

ПРЕОБРАЗОВАНИЕ ИЗ ПОЛЯРНЫХ В ДЕКРАТОВЫХ

Если мы знаем точку в полярных координатах (r, θ) и хотим преобразовать ее в декартовы координаты (x, y), мы решаем прямоугольный треугольник с известными гипотенузой и углом.

Например: преобразовать (13, 22,6°) в декартовы координаты.

РЕШЕНИЕ

Используйте функцию косинуса для x: \(\cos 22.6⁰ = \frac{x}{13}\)

х = \(13 \times \cos 22.6⁰\)

х = 13 × 0,923

х = 12,002

х = 12 (округлить)

Используйте функцию синуса для y: \(\sin 22.6⁰ = \frac{y}{13}\)

у = 13 × \(\sin 22.6⁰\)

у = 13 × 0,391

у = 4,996

у = 5 (округлить)

Ответ: точка (13, 22,6°) равна (12, 5) в декартовых координатах.