Back to the topics list

kuratibu za polar

Uratibu wa polar ni njia ya kuwakilisha nukta katika nafasi.

A- Pole

B- Mhimili wa Polar

r- Radial Coordinate

θ - Uratibu wa Angular

Mfumo wa kuratibu wa polar unarejelea mfumo wa kuratibu wa pande mbili ambapo kila hatua kwenye ndege inathiriwa na umbali kutoka kwa uhakika na pembe kutoka kwa mwelekeo wa kumbukumbu. Kwa hivyo katika kuratibu za Polar, tunazungumza juu ya umbali wa hatua kutoka kwa pole A ambayo inawakilishwa hapa kama r, na pembe ambayo hufanya na mhimili kufikia hatua D ambayo ni θ hapa.

Sehemu ya marejeleo (ambayo ni sawa na asili ya mfumo wa kuratibu wa Cartesian) inajulikana kama pole . Mwale kutoka kwenye nguzo katika mwelekeo wa marejeleo ndio unaojulikana kama mhimili wa polar . Radius, umbali wa radial, au uratibu wa radial ni umbali kutoka kwa nguzo. Pembe kutoka kwa nguzo inajulikana kama azimuth , pembe ya polar, au kuratibu ya angular.

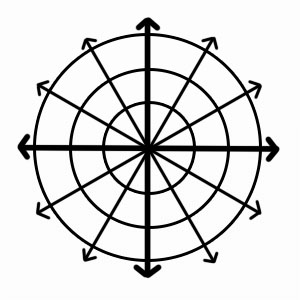
Ili kufafanua hatua katika kuratibu za polar, tunatumia nukuu (r, θ), ambapo r ni umbali kutoka asili hadi uhakika, na θ ni pembe iliyopimwa kinyume cha saa kutoka kwa mhimili wa polar hadi mstari unaounganisha asili kwa uhakika. .

Ili kubadilisha kati ya kuratibu za polar na mstatili (mfumo wa jadi (x, y)), tunatumia fomula zifuatazo:

\(x = r \times \cosθ\)

\(y = r \times \sinθ\)

Kinyume chake, kubadilisha kutoka kwa kuratibu za mstatili hadi kuratibu za polar, tunatumia fomula:

\(r = \sqrt{x^2 + y^2}\)

\(θ = \tan^{-1}{\frac{y}{x}}\)

Hapa, tani ^-1 ni chaguo la kukokotoa ambalo huchukua hoja mbili (y na x) na kurudisha pembe kati ya mhimili wa x chanya na mstari unaopita kwenye asili na (x, y), kupimwa kinyume cha saa.

Viwianishi vya polar ni muhimu sana katika hali zinazohusisha ulinganifu wa mviringo au wa mzunguko, kama vile kuelezea nafasi za pointi kwenye gurudumu au kusogezwa kwa pendulum. Pia hutumiwa sana katika fizikia na uhandisi kuelezea mwendo wa vitu katika kuratibu za polar, kama vile satelaiti zinazozunguka dunia.

KUWAONGOZA

Ili kubadilisha moja kutoka kwa uratibu wa polar hadi uratibu wa Cartesian au kinyume chake, tunatumia pembetatu.

KUBADILISHA KUTOKA CARTESIAN KUWA POLAR

Iwapo tutajua nukta katika Viwianishi vya Cartesian (x, y) na tunataka kuibadilisha kuwa viwianishi vya polar (r, θ), tunaanza kwa kutatua pembetatu ya kulia yenye pande mbili zinazojulikana.

Kwa mfano, (12, 5) ni nini katika Kuratibu za polar?

SULUHISHO

Tumia Theorem ya Pythagoras kupata upande mrefu (hypotenuse).

r ² = 12 ² + 5 ²

r ² = 169

r = 13

Hatua ya pili ni kutumia kazi ya tangent kupata pembe,

\(\tanθ = {5 \over 12}\)

\(θ = \tan^{-1} {\frac{5}{12}} = 22.6⁰ \) (kwa nukta moja ya desimali).

Jibu: Hatua (12,5) ni (13, 22.6 °) katika Kuratibu za Polar.

KUBADILISHA KUTOKA POLAR HADI CARTESIAN

Iwapo tutajua nukta katika Viwianishi vya Polar (r, θ), na tunataka kuibadilisha kuwa Viwianishi vya Cartesian (x,y), tutatatua pembetatu ya kulia kwa hypotenuse na pembe inayojulikana.

Kwa mfano: badilisha (13, 22.6°) hadi Viwianishi vya Cartesian.

SULUHISHO

Tumia Kitendaji cha Cosine cha x: \(\cos 22.6⁰ = \frac{x}{13}\)

x = \(13 \times \cos 22.6⁰\)

x = 13 × 0.923

x = 12.002

x = 12 (zimezimwa)

Tumia Sine Function kwa y: \(\sin 22.6⁰ = \frac{y}{13}\)

y = 13 × \(\sin 22.6⁰\)

y = 13 × 0.391

y = 4.996

y = 5 (kumaliza)

Jibu: Hatua (13, 22.6 °) ni (12, 5) katika Kuratibu za Cartesian.