Back to the topics list

mga coordinate ng polar

Ang polar coordinate ay isang paraan upang kumatawan sa isang punto sa espasyo.

A- Pole

B- Polar Axis

r- Radial Coordinate

θ - Angular Coordinate

Ang polar coordinate system ay tumutukoy sa isang two-dimensional coordinate system kung saan ang bawat punto sa isang eroplano ay naiimpluwensyahan ng isang distansya mula sa isang punto ng sanggunian at isang anggulo mula sa isang direksyon ng sanggunian. Kaya sa Polar coordinates, pinag-uusapan natin ang distansya ng punto mula sa poste A na kinakatawan dito bilang r, at ang anggulo na ginagawa nito sa axis upang maabot ang punto D na θ dito.

Ang reference point (na kahalintulad sa pinagmulan ng isang Cartesian coordinate system) ay tinutukoy bilang pole . Ang sinag mula sa poste sa direksyon ng sanggunian ay tinatawag na polar axis . Ang radius, radial distance, o radial coordinate ay ang distansya mula sa poste. Ang anggulo mula sa pole ay tinutukoy bilang ang azimuth , polar angle, o angular coordinate.

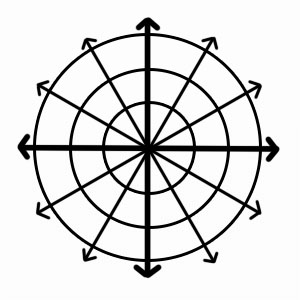
Upang tukuyin ang isang punto sa mga polar coordinate, ginagamit namin ang notasyon (r, θ), kung saan ang r ay ang distansya mula sa pinanggalingan hanggang sa punto, at ang θ ay ang anggulo na sinusukat pakaliwa mula sa polar axis hanggang sa linya na nagkokonekta sa pinanggalingan sa punto. .

Upang mag-convert sa pagitan ng polar at rectangular na coordinate (ang tradisyonal na (x, y) system), ginagamit namin ang mga sumusunod na formula:

\(x = r \times \cosθ\)

\(y = r \times \sinθ\)

Sa kabaligtaran, upang i-convert mula sa hugis-parihaba na mga coordinate sa mga polar na coordinate, ginagamit namin ang mga formula:

\(r = \sqrt{x^2 + y^2}\)

\(θ = \tan^{-1}{\frac{y}{x}}\)

dito, kayumanggi ^-1 ay isang function na kumukuha ng dalawang argumento (y at x) at ibinabalik ang anggulo sa pagitan ng positibong x-axis at ang linyang dumadaan sa pinanggalingan at (x, y), na sinusukat sa counterclockwise.

Ang mga polar coordinate ay partikular na kapaki-pakinabang sa mga sitwasyong kinasasangkutan ng circular o rotational symmetry, gaya ng paglalarawan sa mga posisyon ng mga punto sa isang gulong o paggalaw ng isang pendulum. Ginagamit din ang mga ito nang husto sa pisika at inhinyero upang ilarawan ang paggalaw ng mga bagay sa mga polar coordinates, tulad ng mga satellite na umiikot sa mundo.

NAGBIBIGAY

Upang i-convert ang isa mula sa isang polar coordinate sa isang Cartesian coordinate o vice versa, gumagamit kami ng isang tatsulok.

PAG-convert mula sa CARTESIAN tungo sa POLAR

Kung sakaling may alam tayong punto sa Cartesian Coordinates (x, y) at nais nating i-convert ito sa polar coordinates (r, θ), magsisimula tayo sa pamamagitan ng paglutas ng right triangle na may dalawang panig na kilala.

Halimbawa, Ano ang (12, 5) sa polar Coordinates?

SOLUSYON

Gamitin ang Pythagoras Theorem upang mahanap ang mahabang bahagi (hypotenuse).

r ² = 12 ² + 5 ²

r ² = 169

r = 13

Ang ikalawang hakbang ay ang paggamit ng tangent function upang mahanap ang anggulo,

\(\tanθ = {5 \over 12}\)

\(θ = \tan^{-1} {\frac{5}{12}} = 22.6⁰ \) (sa isang decimal point).

Sagot: Ang punto (12,5) ay (13, 22.6°) sa Polar Coordinates.

PAG-convert MULA POLAR HANGGANG CARTESIAN

Kung sakaling may alam tayong punto sa Polar Coordinates (r, θ), at nais naming i-convert ito sa Cartesian Coordinates (x,y), nilulutas namin ang isang right triangle na may kilalang hypotenuse at anggulo.

Halimbawa: i-convert (13, 22.6°) sa Cartesian Coordinates.

SOLUSYON

Gamitin ang Cosine Function para sa x: \(\cos 22.6⁰ = \frac{x}{13}\)

x = \(13 \times \cos 22.6⁰\)

x = 13 × 0.923

x = 12.002

x = 12 (round off)

Gamitin ang Sine Function para sa y: \(\sin 22.6⁰ = \frac{y}{13}\)

y = 13 × \(\sin 22.6⁰\)

y = 13 × 0.391

y = 4.996

y = 5 (round off)

Sagot: Ang punto (13, 22.6°) ay (12, 5) sa Cartesian Coordinates.