Um einen Bruch zu reduzieren, teilen Sie oben und unten durch die höchste Zahl, die genau in beide Zahlen geteilt werden kann. Das Reduzieren von Brüchen wird auch als Vereinfachen von Brüchen bezeichnet.
Das Reduzieren (oder Vereinfachen) von Brüchen bedeutet, die Brüche so einfach wie möglich zu gestalten.
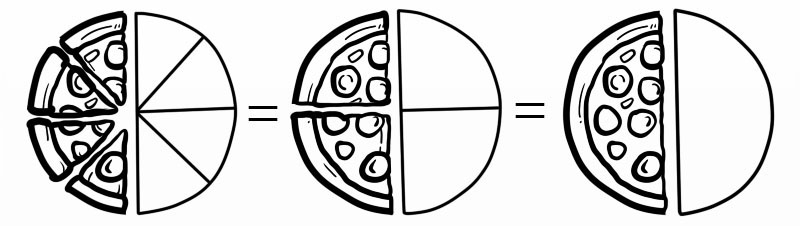
Wenn wir zum Beispiel vier Achtel (4/8) sagen, meinen wir wirklich (1/2)
Es gibt zwei Möglichkeiten, einen Bruch zu vereinfachen:
Methode 1
Versuchen Sie, sowohl den oberen als auch den unteren Teil des Bruchs durch 2, 3,5, 7 usw. zu teilen (nur ganze Zahlen antworten), bis wir nicht mehr weiter gehen können.
Beispiel: Reduzieren Sie den Anteil 24/108:
24/108 = 12/54 = 6/27 = 2/9
Das ist so weit wie wir gehen können. Der Bruch vereinfacht sich zu 2/9.
Beispiel: Reduzieren Sie den Bruch 10/35:
Das Teilen durch 2 funktioniert nicht, da 35 nicht genau durch 2 geteilt werden kann.
Ebenso können wir nicht genau durch 3 teilen.
Keine Notwendigkeit, 4 zu überprüfen (wir haben bereits 2 überprüft, und 4 ist nur 2 × 2).
Aber 5 funktioniert!
10/35 = 2/7
Das ist so weit wie wir gehen können. Der Bruch vereinfacht sich zu 2/7.
Beachten Sie, dass wir nach Überprüfung von 2 nicht 4 überprüfen mussten (4 = 2 × 2)
Wir müssen auch nicht 6 überprüfen, wenn wir 2 und 3 überprüft haben (6 ist 2 × 3)
Tatsächlich verwenden wir bei der Überprüfung vom kleinsten zum größten Primzahlen:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 …………
Methode 2
Teilen Sie die Ober- und Unterseite der Fraktion durch den größten gemeinsamen Faktor (Sie müssen es zuerst herausfinden!).
Beispiel: Reduzieren Sie den Bruch 8/12:
Die größte Zahl, die genau in 8 und 12 geht, ist 4, also ist der größte gemeinsame Faktor 4.
Teilen Sie oben und unten durch 4:
8/12 = 2/3
Das ist so weit wie wir gehen können. Der Bruch vereinfacht sich zu 2/3.