Para reducir una fracción, divida la parte superior e inferior entre el número más alto que puede dividirse en ambos números exactamente. La reducción de fracciones también se conoce como fracciones simplificadoras.
Reducir (o simplificar) las fracciones significa hacer que las fracciones sean lo más simples posible.
Por ejemplo, cuando decimos cuatro octavos (4/8) realmente queremos decir (1/2)
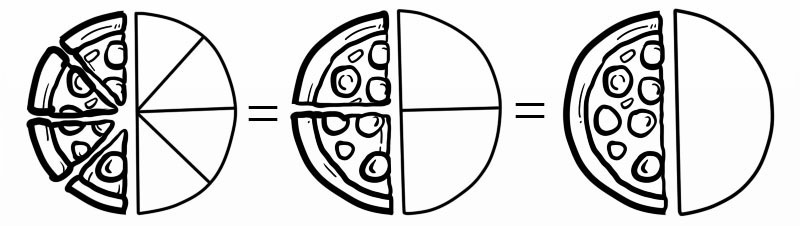
Hay dos formas de simplificar una fracción:
Método 1
Trate de dividir exactamente (solo los números enteros responden) tanto la parte superior como la inferior de la fracción por 2, 3,5, 7, ... etc., hasta que no podamos avanzar más.
Ejemplo: reducir la fracción 24/108:
24/108 = 12/54 = 6/27 = 2/9
Eso es lo más lejos que podemos llegar. La fracción se simplifica a 2/9.
Ejemplo: reducir la fracción 10/35:
Dividir entre 2 no funciona porque 35 no se puede dividir exactamente por 2.
Del mismo modo, no podemos dividir exactamente por 3.
No es necesario verificar 4 (ya verificamos 2, y 4 es solo 2 × 2).
¡Pero 5 funciona!
10/35 = 2/7
Eso es lo más lejos que podemos llegar. La fracción se simplifica a 2/7.
Tenga en cuenta que después de marcar 2 no necesitamos verificar 4 (4 = 2 × 2)
Tampoco necesitamos marcar 6 cuando hemos marcado 2 y 3 (6 es 2 × 3)
De hecho, cuando verificamos de menor a mayor, usamos números primos:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 …………
Método 2
Divide la parte superior e inferior de la fracción por el máximo común divisor (¡primero debes resolverlo!)
Ejemplo: reducir la fracción 8/12:
El número más grande que va exactamente entre 8 y 12 es 4, por lo que el máximo común divisor es 4.
Divide la parte superior e inferior entre 4:
8/12 = 2/3
Eso es lo más lejos que podemos llegar. La fracción se simplifica a 2/3.