Pour réduire une fraction, divisez le haut et le bas par le nombre le plus élevé pouvant être divisé exactement en deux. La réduction des fractions est également connue sous le nom de fractions de simplification.
Réduire (ou simplifier) les fractions signifie rendre les fractions aussi simples que possible.
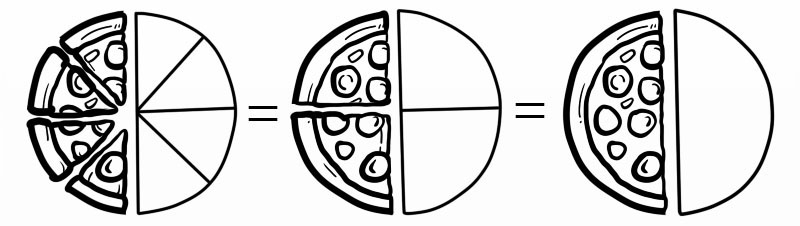
Par exemple, quand nous disons quatre huitièmes (4/8), nous voulons vraiment dire (1/2)
Il existe deux façons de simplifier une fraction:
Méthode 1
Essayez de diviser exactement (uniquement des nombres entiers) le haut et le bas de la fraction par 2, 3,5, 7,… ..etc, jusqu'à ce que nous ne puissions pas aller plus loin.
Exemple: Réduisez la fraction 24/108:
24/108 = 12/54 = 6/27 = 2/9
C'est aussi loin que nous pouvons aller. La fraction se simplifie à 2/9.
Exemple: Réduisez la fraction 10/35:
La division par 2 ne fonctionne pas car 35 ne peut pas être exactement divisé par 2.
De même, nous ne pouvons pas diviser exactement par 3.
Pas besoin de vérifier 4 (nous avons déjà vérifié 2, et 4 est juste 2 × 2).
Mais 5 fonctionne!
10/35 = 2/7
C'est loin que nous pouvons aller. La fraction se simplifie à 2/7.
Notez qu'après avoir vérifié 2, nous n'avons pas eu besoin de vérifier 4 (4 = 2 × 2)
Nous n'avons pas non plus besoin de vérifier 6 lorsque nous avons vérifié 2 et 3 (6 est 2 × 3)
En fait, lors de la vérification du plus petit au plus grand, nous utilisons des nombres premiers:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 …………
Méthode 2
Divisez le haut et le bas de la fraction par le plus grand facteur commun (vous devez d'abord le résoudre!)
Exemple: Réduisez la fraction 8/12:
Le plus grand nombre qui va exactement dans 8 et 12 est 4, donc le plus grand facteur commun est 4.
Divisez le haut et le bas par 4:
8/12 = 2/3
C'est loin que nous pouvons aller. La fraction se simplifie à 2/3.