एक अंश को कम करने के लिए, ऊपर और नीचे को उच्चतम संख्या से विभाजित करें जो दोनों संख्याओं में बिल्कुल विभाजित कर सकते हैं। भिन्नों को कम करना भी भिन्नों को सरल बनाने के रूप में जाना जाता है।
भिन्नों को कम करना (या सरलीकृत करना) का अर्थ है भिन्नों को यथासंभव सरल बनाना।
उदाहरण के लिए, जब हम चार-शब्द (4/8) कहते हैं, तो हम वास्तव में मतलब (1/2)
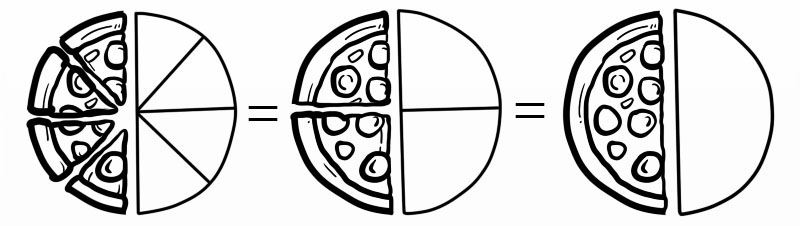
एक अंश को सरल बनाने के दो तरीके हैं:
विधि 1
2, 3,5, 7,… ..etc द्वारा भिन्न के शीर्ष और तल दोनों को (केवल पूरे संख्याओं के उत्तर) में विभाजित करने का प्रयास करें, जब तक कि हम आगे नहीं जा सकते।
उदाहरण: 24/108 अंश को कम करें:
24/108 = 12/54 = 6/27 = 2/9
हम जहां तक जा सकते हैं। अंश 2/9 पर सरल हो जाता है।
उदाहरण: भिन्न को 10/35 घटाएं:
2 से विभाजित करना काम नहीं करता है क्योंकि 35 को 2 से विभाजित नहीं किया जा सकता है।
इसी तरह, हम 3 से बिल्कुल विभाजित नहीं कर सकते।
4 की जांच करने की आवश्यकता नहीं है (हमने पहले से ही 2 की जाँच की, और 4 सिर्फ 2 × 2 है)।
लेकिन 5 काम करता है!
10/35 = 2/7
हम दूर जा सकते हैं। अंश 2/7 तक सरल हो जाता है।
ध्यान दें कि 2 की जाँच के बाद हमें 4 (4 = 2 × 2) की जाँच करने की आवश्यकता नहीं थी
जब हम 2 और 3 की जाँच कर चुके होते हैं तो हमें 6 की जाँच करने की आवश्यकता नहीं होती है (6 2 × 3 है)
वास्तव में, जब छोटी से लेकर बड़ी जाँच हम अभाज्य संख्याओं का उपयोग करते हैं:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 …………
विधि 2
ग्रेटेस्ट कॉमन फैक्टर द्वारा अंश के ऊपर और नीचे को विभाजित करें (आपको इसे पहले काम करना होगा!)
उदाहरण: भिन्न को कम करें 8/12:
सबसे बड़ी संख्या जो 8 और 12 दोनों में होती है, 4 है, इसलिए ग्रेटेस्ट कॉमन फैक्टर 4 है।
ऊपर और नीचे दोनों को 4 से विभाजित करें:
8/12 = 2/3
हम दूर जा सकते हैं। अंश 2/3 को सरल करता है।