Per ridurre una frazione, dividi la parte superiore e inferiore per il numero più alto che può dividere esattamente in entrambi i numeri. La riduzione delle frazioni è anche nota come semplificazione delle frazioni.
Ridurre (o semplificare) le frazioni significa rendere le frazioni il più semplici possibile.
Ad esempio, quando diciamo quattro ottavi (4/8) in realtà intendiamo (1/2)
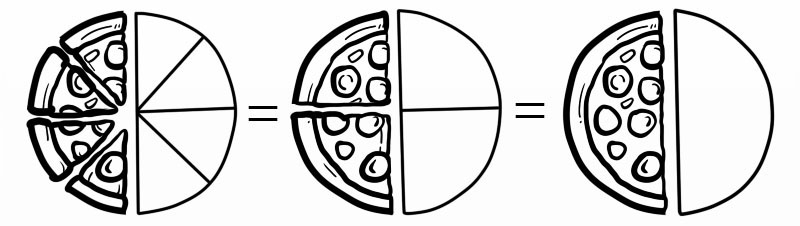
Ci sono due modi per semplificare una frazione:
Metodo 1
Prova a dividere esattamente (risponde solo numeri interi) sia la parte superiore che quella inferiore della frazione per 2, 3,5, 7,…..etc, finché non possiamo andare oltre.
Esempio: ridurre la frazione 24/108:
24/108 = 12/54 = 6/27 = 2/9
Questo è quanto possiamo andare. La frazione si semplifica in 2/9.
Esempio: ridurre la frazione 10/35:
La divisione per 2 non funziona perché 35 non può essere diviso esattamente per 2.
Allo stesso modo, non possiamo dividere esattamente per 3.
Non è necessario controllare 4 (abbiamo già controllato 2 e 4 è solo 2 × 2).
Ma 5 funziona!
10/35 = 2/7
Questo è quanto possiamo andare. La frazione si semplifica in 2/7.
Si noti che dopo aver controllato 2 non abbiamo avuto bisogno di controllare 4 (4 = 2×2)
Inoltre, non abbiamo bisogno di controllare 6 quando abbiamo controllato 2 e 3 (6 è 2×3)
Infatti, controllando dal più piccolo al più grande usiamo i numeri primi:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37…………
Metodo 2
Dividi la parte superiore e inferiore della frazione per il massimo comun divisore (devi prima calcolarlo!)
Esempio: ridurre la frazione 8/12:
Il numero più grande che sta esattamente sia in 8 che in 12 è 4, quindi il massimo comune divisore è 4.
Dividi sia in alto che in basso per 4:
8/12 = 2/3
Questo è quanto possiamo andare. La frazione si semplifica in 2/3.