အပိုင်းခွဲတစ်ခုကို လျှော့ချရန်၊ ဂဏန်းနှစ်ခုလုံးကို အတိအကျခွဲပေးနိုင်သော အမြင့်ဆုံးနံပါတ်ဖြင့် အပေါ်နှင့်အောက်ခြေကို ပိုင်းခြားပါ။ အပိုင်းများကို လျှော့ချခြင်းကို ရိုးရှင်းသောအပိုင်းကိန်းများဟုလည်း ခေါ်သည်။
အပိုင်းများကို လျှော့ချခြင်း (သို့မဟုတ်) ရိုးရိုးရှင်းရှင်း ဆိုသည်မှာ အပိုင်းကိန်းများကို တတ်နိုင်သမျှ ရိုးရှင်းစေရန် ဆိုလိုသည်။
ဥပမာအားဖြင့် လေး-ရှစ် (၄/၈) လို့ ပြောတဲ့အခါ တကယ်ဆို (၁/၂)၊
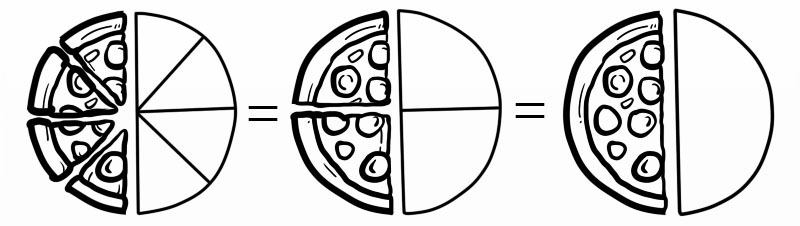
အပိုင်းတစ်ခုကို ရိုးရှင်းအောင်ပြုလုပ်ရန် နည်းလမ်းနှစ်ခုရှိသည်။
နည်းလမ်း ၁
အပိုင်းလေး၏ အပေါ်နှင့်အောက်ခြေကို ၂၊ ၃၊၅၊ ၇၊…..စသည်ဖြင့် ခွဲခြမ်း၍ မရမချင်း (ဂဏန်းအားလုံးအတွက်သာ အဖြေများ) ကို အတိအကျခွဲကြည့်ပါ။
ဥပမာ- အပိုင်းကို 24/108 လျှော့ပါ-
24/108 = 12/54 = 6/27 = 2/9
အဲဒါက ကျနော်တို့ တတ်နိုင်သလောက်တော့ ရှိတယ်။ အပိုင်းကိန်းသည် 2/9 သို့ ရိုးရှင်းသည်။
ဥပမာ- အပိုင်း ၁၀/၃၅ ကို လျှော့ပါ-
35 ကို 2 ဖြင့် အတိအကျ မခွဲနိုင်သောကြောင့် 2 ဖြင့် ပိုင်းခြင်း အလုပ်မဖြစ်ပါ။
ဒီလိုပဲ အတိအကျ ၃ နဲ့ ခွဲလို့မရဘူး။
4 ကိုစစ်ဆေးရန်မလိုအပ်ပါ (ကျွန်ုပ်တို့သည် 2 ကိုစစ်ဆေးပြီးဖြစ်သည်၊ 4 သည် 2 × 2 ဖြစ်သည်)။
ဒါပေမယ့် 5 ကအလုပ်လုပ်တယ်။
10/35 = 2/7
အဲဒါက ကျနော်တို့ တတ်နိုင်သလောက်တော့ ရှိတယ်။ အပိုင်းကိန်းသည် 2/7 သို့ ရိုးရှင်းသည်။
2 ကိုစစ်ဆေးပြီးနောက် 4 (4 = 2 × 2) ကိုစစ်ဆေးရန်မလိုအပ်ကြောင်းသတိပြုပါ။
2 နှင့် 3 ကိုစစ်ဆေးသောအခါ 6 ကိုစစ်ဆေးရန်မလိုအပ်ပါ (6 သည် 2 × 3)
အမှန်တော့၊ အငယ်ဆုံးကနေ အကြီးဆုံးကို စစ်ကြည့်တဲ့အခါ အဓိကနံပါတ်တွေကို သုံးပါတယ်။
၂၊ ၃၊ ၅၊ ၇၊ ၁၁၊ ၁၃၊ ၁၇၊ ၁၉၊ ၂၃၊ ၂၉၊ ၃၁၊ ၃၇…………
နည်းလမ်း ၂
အပိုင်း၏အပေါ်နှင့်အောက်ခြေကို အကြီးမြတ်ဆုံးဘုံအချက်ဖြင့် ပိုင်းခြားပါ (၎င်းကို ဦးစွာလုပ်ဆောင်ရန် လိုအပ်ပါသည်။)
ဥပမာ- ၈/၁၂ အပိုင်းကို လျှော့ပါ-
8 နှင့် 12 နှစ်ခုစလုံးတွင် အတိအကျပါဝင်သည့် အကြီးဆုံးဂဏန်းမှာ 4 ဖြစ်ပြီး၊ အကြီးမားဆုံး ဘုံကိန်းမှာ 4 ဖြစ်သည်။
အပေါ်နှင့်အောက်ခြေကို 4 ဖြင့် ပိုင်းပါ။
8/12 = 2/3
အဲဒါက ကျနော်တို့ တတ်နိုင်သလောက်တော့ ရှိတယ်။ အပိုင်းကိန်းသည် 2/3 သို့ ရိုးရှင်းသည်။