अंश घटाउनको लागि, माथि र तल्लो भागलाई उच्चतम संख्याले विभाजन गर्नुहोस् जुन दुबै संख्याहरूमा ठ्याक्कै विभाजित गर्न सकिन्छ। अंशहरू घटाउनुलाई सरलीकृत अंशहरू पनि भनिन्छ।
अंशहरू घटाउनु (वा सरलीकरण) भनेको अंशहरूलाई सकेसम्म सरल बनाउनु हो।
उदाहरण को लागी, जब हामी चार-आठौं (4/8) भन्छौं हामी वास्तवमा (1/2)
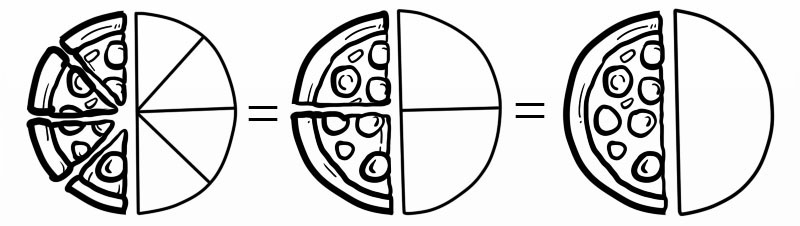
त्यहाँ एक अंश सरल बनाउन दुई तरिकाहरू छन्:
विधि १
ठ्याक्कै भाग गर्ने प्रयास गर्नुहोस् (मात्र पूर्ण संख्याका उत्तरहरू) माथि र तल्लो भागलाई 2, 3,5, 7, ….. आदि द्वारा, जबसम्म हामी अगाडि जान सक्दैनौं।
उदाहरण: अंश 24/108 घटाउनुहोस्:
24/108 = 12/54 = 6/27 = 2/9
त्यो हामी जति टाढा जान सक्छौं। अंशले 2/9 मा सरल बनाउँछ।
उदाहरण: अंश 10/35 घटाउनुहोस्:
2 ले भाग गर्दा काम गर्दैन किनभने 35 लाई 2 ले भाग गर्न सकिँदैन।
त्यस्तै गरी, हामी ठ्याक्कै ३ ले भाग गर्न सक्दैनौं।
4 जाँच गर्न आवश्यक छैन (हामीले पहिले नै 2 जाँच गरेका छौं, र 4 मात्र 2 × 2 हो)।
तर 5 ले काम गर्छ!
१०/३५ = २/७
त्यो हामी जति टाढा जान सक्छौं। अंशले २/७ मा सरल बनाउँछ।
ध्यान दिनुहोस् कि 2 जाँच गरेपछि हामीले 4 (4 = 2×2) जाँच गर्न आवश्यक छैन।
हामीले 2 र 3 (6 भनेको 2×3 हो) जाँच गरिसकेपछि हामीले 6 जाँच गर्नुपर्दैन।
वास्तवमा, सानो देखि ठूलो सम्म जाँच गर्दा हामी अविभाज्य संख्याहरू प्रयोग गर्छौं:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 ………
विधि २
सबैभन्दा ठूलो साझा कारकद्वारा अंशको माथि र तल्लो भाग विभाजन गर्नुहोस् (तपाईंले यसलाई पहिले काम गर्नुपर्छ!)
उदाहरण: अंश 8/12 घटाउनुहोस्:
ठ्याक्कै 8 र 12 दुबैमा जाने सबैभन्दा ठूलो संख्या 4 हो, त्यसैले सबैभन्दा ठूलो सामान्य कारक 4 हो।
माथि र तल दुवैलाई ४ ले विभाजन गर्नुहोस्:
८/१२ = २/३
त्यो हामी जति टाढा जान सक्छौं। अंशले 2/3 लाई सरल बनाउँछ।