Aby skrócić ułamek, podziel górną i dolną część przez największą liczbę, która dokładnie dzieli obie liczby. Skracanie ułamków jest również znane jako upraszczanie ułamków.
Redukcja (lub upraszczanie) ułamków oznacza uczynienie ułamków tak prostymi, jak to tylko możliwe.
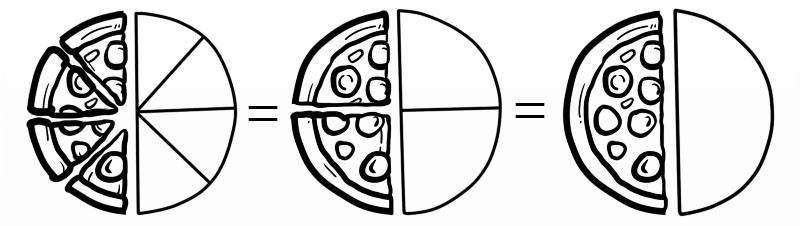
Na przykład, kiedy mówimy cztery ósme (4/8), tak naprawdę mamy na myśli (1/2)
Istnieją dwa sposoby uproszczenia ułamka:
Metoda 1
Spróbuj dokładnie podzielić (odpowiadają tylko liczby całkowite) zarówno górną, jak i dolną część ułamka przez 2, 3,5, 7,…..itp., aż nie będziemy mogli pójść dalej.
Przykład: Zmniejsz ułamek 24/108:
24/108 = 12/54 = 6/27 = 2/9
To jest tak daleko, jak możemy się posunąć. Ułamek upraszcza się do 2/9.
Przykład: Skróć ułamek 10/35:
Dzielenie przez 2 nie działa, ponieważ 35 nie może być dokładnie podzielone przez 2.
Podobnie nie możemy dzielić dokładnie przez 3.
Nie ma potrzeby sprawdzania 4 (sprawdziliśmy już 2, a 4 to tylko 2 × 2).
Ale 5 działa!
10/35 = 2/7
To jest tak daleko, jak możemy iść. Ułamek upraszcza się do 2/7.
Zauważ, że po sprawdzeniu 2 nie musieliśmy sprawdzać 4 (4 = 2×2)
Nie musimy też sprawdzać 6, gdy sprawdziliśmy 2 i 3 (6 to 2×3)
W rzeczywistości, sprawdzając od najmniejszej do największej, używamy liczb pierwszych:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37…………
Metoda 2
Podziel górną i dolną część ułamka przez największy wspólny czynnik (musisz to najpierw obliczyć!)
Przykład: Skróć ułamek 8/12:
Największa liczba, która mieści się dokładnie w 8 i 12, to 4, więc największym wspólnym dzielnikiem jest 4.
Podziel górę i dół przez 4:
8/12 = 2/3
To jest tak daleko, jak możemy iść. Ułamek upraszcza się do 2/3.