หากต้องการลดเศษส่วน ให้แบ่งด้านบนและด้านล่างด้วยจำนวนสูงสุดที่สามารถแบ่งออกเป็นตัวเลขทั้งสองได้อย่างแม่นยำ การลดเศษส่วนเรียกอีกอย่างว่าการลดทอนเศษส่วน
การลดขนาด (หรือการลดรูป) เศษส่วนหมายถึงการทำให้เศษส่วนง่ายที่สุด
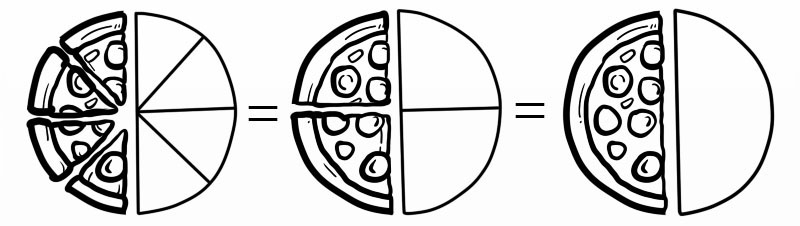
ตัวอย่างเช่น เมื่อเราพูดสี่ในแปด (4/8) เราหมายถึงจริงๆ (1/2)
มีสองวิธีในการทำให้เศษส่วนง่ายขึ้น:
วิธีที่ 1
พยายามหารให้ถูกต้อง (ตอบเฉพาะจำนวนเต็มเท่านั้น) ทั้งบนและล่างของเศษส่วนด้วย 2, 3,5, 7,…..ฯลฯ จนกว่าเราจะไปต่อไม่ได้
ตัวอย่าง: ลดเศษส่วน 24/108:
24/108 = 12/54 = 6/27 = 2/9
นั่นคือเท่าที่เราจะไปได้ เศษส่วนลดรูปเป็น 2/9
ตัวอย่าง: ลดเศษส่วน 10/35:
การหารด้วย 2 ไม่ได้ผลเพราะ 35 ไม่สามารถหารด้วย 2 ได้ทั้งหมด
ในทำนองเดียวกัน เราหารด้วย 3 เป๊ะๆ ไม่ได้
ไม่จำเป็นต้องตรวจสอบ 4 (เราตรวจสอบ 2 แล้วและ 4 เป็นเพียง 2 × 2)
แต่ 5 ใช้งานได้!
10/35 = 2/7
ไกลเท่าที่เราจะไปได้ เศษส่วนลดรูปเป็น 2/7
สังเกตว่าหลังจากตรวจสอบ 2 เราไม่ต้องตรวจสอบ 4 (4 = 2×2)
เรายังไม่ต้องเช็ค 6 เมื่อเราตรวจสอบ 2 และ 3 (6 คือ 2×3)
ที่จริงแล้ว เมื่อตรวจสอบจากน้อยไปมาก เราใช้จำนวนเฉพาะ:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37…………
วิธีที่ 2
หารส่วนบนและส่วนล่างของเศษส่วนด้วยตัวประกอบร่วมที่ยิ่งใหญ่ที่สุด (คุณต้องหาให้เจอก่อน!)
ตัวอย่าง: ลดเศษส่วน 8/12:
จำนวนที่มากที่สุดที่หารทั้ง 8 และ 12 ลงตัวคือ 4 ดังนั้นตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดคือ 4
หารทั้งบนและล่างด้วย 4:
8/12 = 2/3
ไกลเท่าที่เราจะไปได้ เศษส่วนลดรูปเหลือ 2/3