improper fraction

An improper fraction has a top number larger than (or equal to) the bottom number.

Example:

 Where 3 is greater than 2

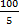 Where 100 is greater than 5

 

A fraction such as   has two numbers - Numerator and Denominator. For example, in    7 is the numerator and 4 is the denominator. This means:

• We have 7 parts.
• Each part is a quarter (1/4) of a whole.

 

Improper Fractions or Mixed Fractions

We can use either an improper fraction or a mixed fraction to show the same amount.

 

For example, 1  =  as shown here

 

Converting improper fractions to mixed fractions

To convert an improper fraction to a mixed fraction, follow these steps:

• Divide the numerator to the denominator. 
• Write down the whole number answer. 
• Then write down any remainder above the denominator. 

Example: Convert 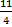 to a mixed fraction

• Divide 11 by 4 i.e. 11 ÷ 4 = 2 with remainder 3.
• Write down the 2 and then write down the remainder (3) above the denominator (4).
• Answer: 2 i.e. Quotient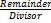

Convert mixed fractions to improper fractions

To convert a mixed fraction to an improper fraction, follow these steps:

• Multiply the whole number part by the fraction’s denominator
• Add that to the numerator
• Then write the result on top of the denominator

Example: Convert 3  to an improper fraction

• Multiply the whole number part by the denominator: 3 × 5 = 15
• Add that to the numerator: 15 + 2 = 17
• Then write that result above the denominator:

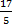
Adding and subtracting improper fractions

The rules for adding and subtracting improper fractions are the same as working with proper fractions.

Adding and subtracting improper fractions with common denominators

Step 1 – Keep the denominator the same.

Step 2 – Add or subtract the numerators.  

Step 3 – If the answer is an improper form, reduce the fraction into a mixed number.

For example,  +   = 

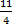
Thus, we have 2

 

Adding and subtracting improper fractions with different denominators

• Find the Lowest Common Multiple (LCM) between the denominators.
• Multiply the numerator and denominator of each fraction by a number so that they have the LCM as their new denominator.
• Add or subtract the numerators and keep the denominator the same.
• If the answer is an improper form, reduce the fraction into a mixed number.

Example: Subtract the fraction  -

• The Lowest Common Multiple between 6 and 8 is 24.
• Find a number that when multiplied to the top and bottom of 76, we get the LCM (24) as the new denominator:  =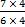
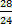
• Find a number that when multiplied to the top and bottom of 3/8, we get the LCM (24) as the new denominator: 3 =
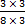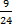
• Since our fractions now have equal-sized slices, we can subtract their numerators. Thus, we now have 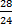 -  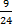 =  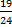of a whole.