Back to the topics list

不適切な分数

仮分数は、一番上の数字が一番下の数字より大きい (または等しい) ものです。

例：

3 が 2 より大きい場合

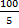100 が 5 より大きい場合

のような分数には、分子と分母の 2 つの数値があります。たとえば、 7 は分子で、4 は分母です。これの意味は：

• 7つのパーツがあります。
• 各部分は全体の 4 分の 1 (1/4) です。

不適切な分数または混合分数

仮分数または帯分数のいずれかを使用して、同じ量を示すことができます。

たとえば、1 =ここに示すように

仮分数を帯分数に変換する

仮分数を帯分数に変換するには、次の手順に従います。

• 分子を分母に割ります。
• 整数の答えを書きなさい。
• 次に、分母の上の残りを書き留めます。

例: 変換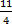混合分数に

• 11 を 4 で割ります。つまり、11 ÷ 4 = 2 余り 3 です。
• 2 を書き留めてから、分母 (4) の上に剰余 (3) を書き留めます。
• 答え: 2つまり、商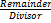

帯分数を仮分数に変換する

混合分数を仮分数に変換するには、次の手順に従います。

• 整数部分に分数の分母を掛けます
• それを分子に追加します
• 次に、分母の上に結果を書き込みます

例: 変換 3不適切な分数に

• 整数部分に分母を掛けます: 3 × 5 = 15
• それを分子に追加します: 15 + 2 = 17
• 次に、その結果を分母の上に書きます。

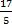
仮分数の足し算と引き算

仮分数の足し算と引き算のルールは、固有分数の計算と同じです。

分母が共通の仮分数のたし算とひき算

ステップ 1 – 分母を同じに保ちます。

ステップ 2 – 分子を加算または減算します。

ステップ 3 – 答えが不適切な形式の場合は、分数を混合数に減らします。

例えば、 + =

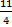
したがって、2

分母が異なる仮分数の足し算と引き算

• 分母間の最小公倍数 (LCM) を見つけます。
• 各分数の分子と分母に数値を掛けて、LCM を新しい分母にします。
• 分子を加算または減算し、分母を同じに保ちます。
• 答えが不適切な形式の場合は、分数を帯分数に減らします。

例: 分数を引く-

• 6 と 8 の間の最小公倍数は 24 です。
• 7 6の上と下に掛けると、LCM (24) を新しい分母として取得します。 =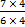
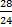
• 3/8 の上下に掛けると、新しい分母として最小公倍数 (24) が得られる数値を見つけます: 3 =
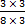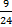
• 分数には同じサイズのスライスがあるため、分子を引くことができます。したがって、私たちは今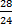- 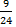=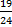全体の。