الكسر المختلط هو عدد صحيح ويمثل الكسر الصحيح معًا. يمثل بشكل عام رقمًا بين أي رقمين صحيحين.
تعرف الكسور المختلطة أيضًا بالأرقام الكسرية.
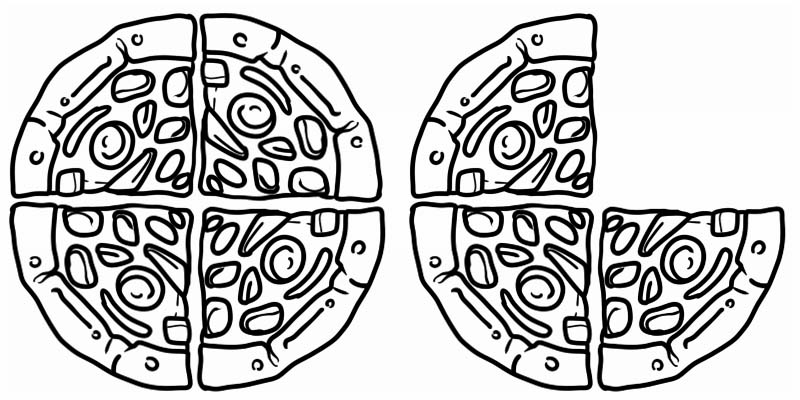
انظر إلى الصورة المعينة التي تمثل كسرًا أكبر من 1 ولكن أقل من 2. فهو بالتالي عدد مختلط يساوي \(1\frac{3}{4}\)
بعض الأمثلة الأخرى للأرقام المختلطة هي:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
يتكون العدد الكسري من الجمع بين ثلاثة أجزاء: عدد صحيح ، وبسط ، ومقام. البسط والمقام جزء من الكسر الصحيح الذي يصنع العدد الكسري.
في العدد المختلط \(3\frac{1}{2}\)
الخطوة 1: اقسم البسط على المقام
الخطوة 2: اكتب حاصل القسمة كرقم صحيح
الخطوة 3: اكتب الباقي على أنه البسط والمقسوم عليه كمقام
على سبيل المثال ، نتبع الخطوات المحددة لتحويل \(\frac{7}{3}\) إلى صيغة عدد مختلط.
الخطوة 1: قسّم 7 على 3
الخطوة 2: اكتب حاصل القسمة والمقسوم عليه والباقي بصيغة العدد المختلط: \(2\frac{1}{3}\)
يمكن للمرء أن يضيف (أو يطرح) أرقامًا مختلطة عن طريق إعادة ترتيب الأعداد الصحيحة ، وإضافتها (أو طرحها) بشكل منفصل وإضافة الكسور المتبقية بشكل فردي وفي النهاية دمجها جميعًا.
\(1\frac{1}{2} + 3\frac{3}{4} \)
جمع الأعداد الصحيحة بشكل منفصل والكسور بشكل منفصل.
للأعداد الصحيحة:
1 + 3 = 4
للكسور: أوجد المضاعف المشترك الأصغر ثم اجمعه
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
تحويل الكسر غير الصحيح إلى عدد كسري: \(\frac{5}{4} = 1\frac{1}{4}\)
في النهاية ، قم بإضافة كلا الجزأين معًا.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
ما عليك سوى اتباع نفس الطريقة (مثل الجمع) ، ولكن اطرح بدلاً من الجمع:
مثال: \(15\frac{3}{4} - 8\frac{5}{6}\)
حوّل إلى كسور غير صحيحة: \(\frac{63}{4} - \frac{53}{6}\)
المقام المشترك (المضاعف المشترك الأصغر للعدد 4 و 6) لـ 12: \(\frac{189}{12} - \frac{106}{12}\)
الآن اطرح: \(\frac{83}{12}\)
التغيير إلى كسر مختلط: \(6\frac{11}{12}\)
مثال: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
مثال:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)