Back to the topics list

qarışıq fraksiya, qarışıq nömrələr

Qarışıq fraksiyalar nədir?

Qarışıq kəsr tam ədəddir və uyğun kəsr birlikdə təmsil olunur. O, ümumiyyətlə hər hansı iki tam ədəd arasındakı ədədi təmsil edir.

Qarışıq kəsrlərə qarışıq ədədlər də deyilir.

Verilmiş şəklə baxın, o, 1-dən böyük, lakin 2-dən kiçik olan kəsri təmsil edir. Beləliklə, qarışıq ədəddir, \(1\frac{3}{4}\)

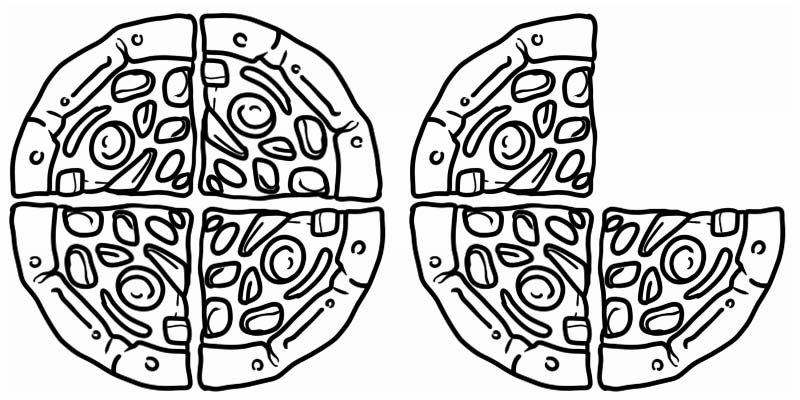
Qarışıq ədədlərin bəzi digər nümunələri bunlardır:

\(3\frac{1}{2}\)

\(2\frac{3}{5}\)

\(5\frac{3}{5}\)

\(4\frac{1}{5}\)

Qarışıq ədədin hissələri

Qarışıq ədəd üç hissənin birləşməsindən əmələ gəlir: tam ədəd, pay və məxrəc. Pay və məxrəc qarışıq ədədi yaradan düzgün kəsrin bir hissəsidir.

Qarışıq \(3\frac{1}{2}\)

• 3 tam ədəddir
• \(\frac{1}{2}\) kəsrdir, burada 1 ədəd, 2 isə məxrəcdir

Qarışıq ədədlərin xassələri

• Bu qismən tam ədəddir
• Bu qismən bir hissədir

Yanlış kəsrin qarışıq kəsrlərə çevrilməsi

Addım 1: Numeratoru məxrəcə bölün

Addım 2: Hissəni tam ədəd kimi yazın

Addım 3: Qalanı pay, bölücü isə məxrəc kimi yazın.

Məsələn, \(\frac{7}{3}\) qarışıq ədəd formasına çevirmək üçün verilən addımları izləyirik.

Addım 1: 7-ni 3-ə bölün

Addım 2: Qarışıq ədəd şəklində bölmə, bölən və qalığı yazın: \(2\frac{1}{3}\)

Qarışıq fraksiyaların əlavə və ya çıxılması

Tam ədədləri yenidən təşkil etməklə, onları ayrıca əlavə etməklə (və ya çıxmaqla) və qalan kəsrləri ayrı-ayrılıqda əlavə etməklə və sonunda hamısını birləşdirərək qarışıq ədədləri əlavə etmək (və ya çıxmaq) olar.

\(1\frac{1}{2} + 3\frac{3}{4} \)

Tam ədədləri ayrıca, kəsrləri isə ayrıca toplamaq.

Tam ədədlər üçün:

1 + 3 = 4

Kəsrlər üçün: LCM-i tapın və sonra əlavə edin

\(\frac{1}{2} + \frac{3}{4}\)

= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)

= \(\frac{2}{4} + \frac{3}{4}\)

= \(\frac{5}{4}\)

Düzgün olmayan kəsri qarışıq ədədə çevirmək: \(\frac{5}{4} = 1\frac{1}{4}\)

Sonda hər iki hissəni birlikdə əlavə edin.

\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)

Qarışıq kəsrlərin çıxarılması

Sadəcə eyni üsula əməl edin (əlavə etmək kimi), lakin əlavə etmək əvəzinə çıxarın:

Misal: \(15\frac{3}{4} - 8\frac{5}{6}\)

Yanlış kəsrlərə çevirin: \(\frac{63}{4} - \frac{53}{6}\)

12-nin ortaq məxrəci (4 və 6-nın LCM): \(\frac{189}{12} - \frac{106}{12}\)

İndi çıxın: \(\frac{83}{12}\)

Qarışıq kəsrə dəyişdirin: \(6\frac{11}{12}\)

Qarışıq fraksiyaların vurulması

• Hər bir qarışıq fraksiyanı düzgün olmayan kəsrə dəyişdirin
• Mümkünsə sadələşdirin
• Sayları, sonra isə məxrəcləri çoxaldın
• Cavabı ən aşağı şərtlərlə qoyun
• Cavabın mənalı olduğundan əmin olmaq üçün yoxlayın

Misal: \(5\frac{2}{3} \times \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{1}{4}\)

= \(\frac{17}{12}\)

= \(1\frac{5}{12}\)

Qarışıq fraksiyaların bölünməsi

• Hər bir qarışıq fraksiyanı düzgün olmayan kəsrə dəyişdirin
• Mümkünsə sadələşdirərək, bölənin əksi ilə vurun
• Cavabı ən aşağı şərtlərlə qoyun
• Cavabın mənalı olduğundan əmin olmaq üçün yoxlayın

Misal:

\(5\frac{2}{3} \div \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{4}{1}\)

= \(\frac{68}{3}\)

= \(22\frac{2}{3}\)