একটি মিশ্র ভগ্নাংশ একটি পূর্ণ সংখ্যা, এবং একটি সঠিক ভগ্নাংশ একসাথে উপস্থাপন করা হয়। এটি সাধারণত যেকোনো দুটি পূর্ণ সংখ্যার মধ্যে একটি সংখ্যাকে উপস্থাপন করে।
মিশ্র ভগ্নাংশগুলি মিশ্র সংখ্যা হিসাবেও পরিচিত।
প্রদত্ত চিত্রটি দেখুন এটি একটি ভগ্নাংশকে প্রতিনিধিত্ব করে যা 1 এর চেয়ে বড় কিন্তু 2 এর কম। এইভাবে এটি একটি মিশ্র সংখ্যা, যা \(1\frac{3}{4}\) সমান।
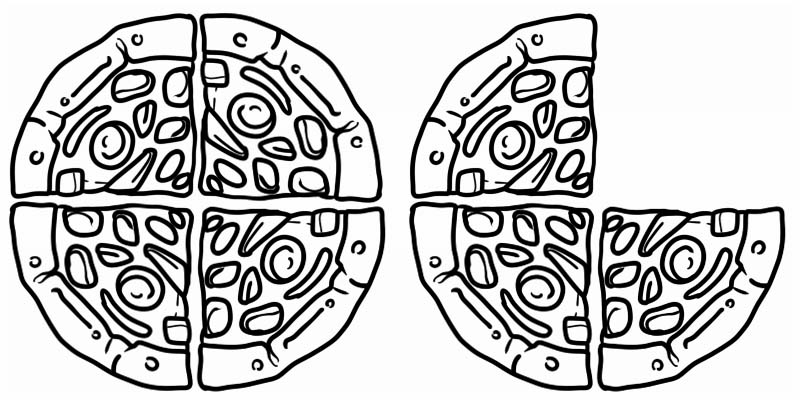
মিশ্র সংখ্যার আরও কিছু উদাহরণ হল:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
একটি মিশ্র সংখ্যা তিনটি অংশের সমন্বয়ে গঠিত হয়: একটি পূর্ণ সংখ্যা, একটি লব এবং একটি হর। লব এবং হর হল সঠিক ভগ্নাংশের অংশ যা মিশ্র সংখ্যা তৈরি করে।
মিশ্র সংখ্যায় \(3\frac{1}{2}\)
ধাপ 1: লবকে হর দ্বারা ভাগ করুন
ধাপ 2: ভাগফলকে পুরো সংখ্যা হিসাবে লিখুন
ধাপ 3: লব হিসাবে অবশিষ্টাংশ এবং হর হিসাবে ভাজক লিখুন
উদাহরণস্বরূপ, আমরা \(\frac{7}{3}\) একটি মিশ্র সংখ্যা আকারে রূপান্তর করার জন্য প্রদত্ত পদক্ষেপগুলি অনুসরণ করি।
ধাপ 1: 7 কে 3 দ্বারা ভাগ করুন
ধাপ 2: ভাগফল, ভাজক এবং অবশিষ্টাংশ মিশ্র সংখ্যা আকারে লিখুন: \(2\frac{1}{3}\)
কেউ মিশ্র সংখ্যা যোগ (বা বিয়োগ) করতে পারে সম্পূর্ণ সংখ্যাগুলিকে পুনর্বিন্যাস করে, আলাদাভাবে যোগ করে (বা বিয়োগ করে) এবং অবশিষ্ট ভগ্নাংশগুলিকে পৃথকভাবে যোগ করে এবং শেষ পর্যন্ত সেগুলিকে একত্রিত করে।
\(1\frac{1}{2} + 3\frac{3}{4} \)
সম্পূর্ণ সংখ্যা আলাদাভাবে এবং ভগ্নাংশগুলোকে আলাদাভাবে যোগ করা।
পূর্ণ সংখ্যার জন্য:
1 + 3 = 4
ভগ্নাংশের জন্য: LCM খুঁজুন এবং তারপর যোগ করুন
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
অনুপযুক্ত ভগ্নাংশকে একটি মিশ্র সংখ্যায় রূপান্তর করা হচ্ছে: \(\frac{5}{4} = 1\frac{1}{4}\)
শেষ পর্যন্ত, উভয় অংশ একসাথে যোগ করুন।
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
শুধু একই পদ্ধতি অনুসরণ করুন (যেমন যোগ করার জন্য), কিন্তু যোগ করার পরিবর্তে বিয়োগ করুন:
উদাহরণ: \(15\frac{3}{4} - 8\frac{5}{6}\)
অনুপযুক্ত ভগ্নাংশে রূপান্তর করুন: \(\frac{63}{4} - \frac{53}{6}\)
12-এর সাধারণ হর (4 এবং 6-এর LCM): \(\frac{189}{12} - \frac{106}{12}\)
এখন বিয়োগ করুন: \(\frac{83}{12}\)
একটি মিশ্র ভগ্নাংশে পরিবর্তন করুন: \(6\frac{11}{12}\)
উদাহরণ: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
উদাহরণ:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)