Ein gemischter Bruch ist eine ganze Zahl und ein echter Bruch zusammen dargestellt. Es stellt im Allgemeinen eine Zahl zwischen zwei beliebigen ganzen Zahlen dar.
Gemischte Brüche werden auch als gemischte Zahlen bezeichnet.
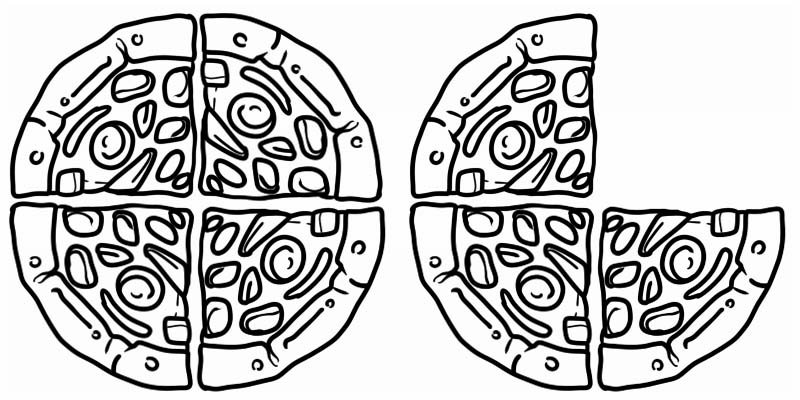
Schauen Sie sich das gegebene Bild an, es stellt einen Bruch dar, der größer als 1, aber kleiner als 2 ist. Es ist also eine gemischte Zahl, gleich \(1\frac{3}{4}\)
Einige andere Beispiele für gemischte Zahlen sind:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Eine gemischte Zahl wird gebildet, indem drei Teile kombiniert werden: eine ganze Zahl, ein Zähler und ein Nenner. Zähler und Nenner sind Teil des richtigen Bruchs, der die gemischte Zahl ergibt.
In der gemischten Zahl \(3\frac{1}{2}\)
Schritt 1: Teile den Zähler durch den Nenner
Schritt 2: Notieren Sie den Quotienten als ganze Zahl
Schritt 3: Schreibe den Rest als Zähler und den Divisor als Nenner auf
Zum Beispiel folgen wir den angegebenen Schritten, um \(\frac{7}{3}\) in eine gemischte Zahlenform umzuwandeln.
Schritt 1: Teilen Sie 7 durch 3
Schritt 2: Quotient, Divisor und Rest in gemischter Zahlenform schreiben: \(2\frac{1}{3}\)
Man kann gemischte Zahlen addieren (oder subtrahieren), indem man die ganzen Zahlen neu anordnet, sie einzeln addiert (oder subtrahiert) und die übrig gebliebenen Brüche einzeln addiert und am Ende alle kombiniert.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Die ganzen Zahlen separat und die Brüche separat addieren.
Für ganze Zahlen:
1 + 3 = 4
Für Brüche: LCM finden und dann addieren
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Umwandlung des unechten Bruchs in eine gemischte Zahl: \(\frac{5}{4} = 1\frac{1}{4}\)
Fügen Sie am Ende beide Teile zusammen.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Folgen Sie einfach der gleichen Methode (wie beim Addieren), aber subtrahieren Sie anstatt zu addieren:
Beispiel: \(15\frac{3}{4} - 8\frac{5}{6}\)
In unechte Brüche umwandeln: \(\frac{63}{4} - \frac{53}{6}\)
Der gemeinsame Nenner (LCM von 4 und 6) von 12: \(\frac{189}{12} - \frac{106}{12}\)
Jetzt subtrahieren: \(\frac{83}{12}\)
Umwandlung in einen gemischten Bruch: \(6\frac{11}{12}\)
Beispiel: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Beispiel:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)