mixed fraction, mixed numbers

What are mixed fractions?

A mixed fraction is a whole number, and a proper fraction represented together. It generally represents a number between any two whole numbers.

Mixed fractions are also known as mixed numbers.

Look at the given image it represents a fraction that is greater than 1 but less than 2. It is thus, a mixed number, equal to \(1\frac{3}{4}\)

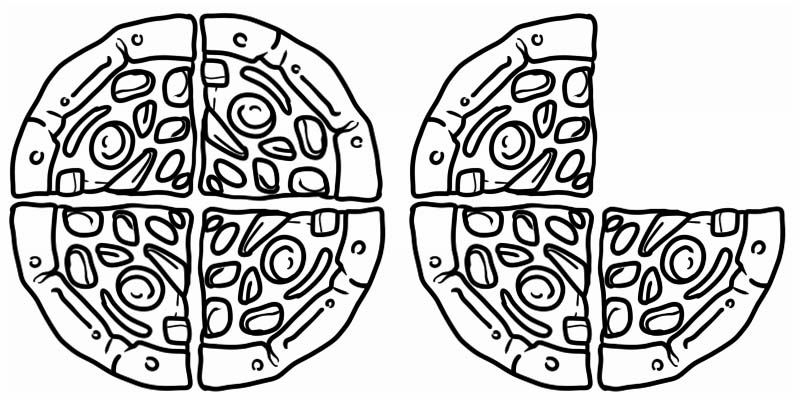
Some other examples of mixed numbers are:

\(3\frac{1}{2}\)

\(2\frac{3}{5}\)

\(5\frac{3}{5}\)

\(4\frac{1}{5}\)

Parts of a mixed number

A mixed number is formed by combining three parts: a whole number, a numerator, and a denominator. The numerator and denominator are part of the proper fraction that makes the mixed number.

In the mixed number \(3\frac{1}{2}\)

• 3 is the whole number
• \(\frac{1}{2}\) is a fraction, where 1 is the numerator and 2 is the denominator

 

Properties of mixed numbers

• It is partly a whole number
• It is partly a fraction

Converting improper fraction to mixed fractions

Step 1: Divide the numerator by the denominator

Step 2: Write down the quotient as the whole number

Step 3: Write down the remainder as the numerator and the divisor as the denominator

For example, we follow the given steps to convert \(\frac{7}{3}\) into a mixed number form.

Step 1: Divide 7 by 3

Step 2: Write quotient, divisor and remainder in the mixed number form: \(2\frac{1}{3}\)

Adding or subtracting mixed fractions

One can add (or subtract) mixed numbers by rearranging the whole numbers, adding (or subtracting) them separately and adding the leftover fractions individually and in the end combining them all.

\(1\frac{1}{2} + 3\frac{3}{4} \)

Adding the whole numbers separately and the fractions separately.

For whole numbers:

1 + 3 = 4

For fractions: Find the LCM and then add

\(\frac{1}{2} + \frac{3}{4}\)

= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)

= \(\frac{2}{4} + \frac{3}{4}\)

= \(\frac{5}{4}\)

 

Converting the improper fraction into a mixed number: \(\frac{5}{4} = 1\frac{1}{4}\)

In the end, adding both the parts together.

\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)

Subtracting mixed fractions

Just follow the same method (like for adding), but subtract instead of add:

Example: \(15\frac{3}{4} - 8\frac{5}{6}\)

Convert to improper fractions: \(\frac{63}{4} - \frac{53}{6}\)

The common denominator (LCM of 4 and 6) of 12: \(\frac{189}{12} - \frac{106}{12}\)

Now subtract:  \(\frac{83}{12}\)

Change into a mixed fraction:  \(6\frac{11}{12}\)

 

Multiplying mixed fractions

• Change each mixed fraction to an improper fraction
• Simplify if possible
• Multiply the numerators and then the denominators
• Put the answer in lowest terms
• Check to be sure the answer makes sense

Example: \(5\frac{2}{3} \times \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{1}{4}\)

= \(\frac{17}{12}\)

= \(1\frac{5}{12}\)

Dividing mixed fractions

• Change each mixed fraction to an improper fraction
• Multiply by the reciprocal of the divisor, simplifying if possible
• Put the answer in lowest terms
• Check to be sure the answer makes sense

Example:

\(5\frac{2}{3} \div \frac{1}{4}\)

=\(\frac{17}{3} \times \frac{4}{1}\)

=\(\frac{68}{3}\)

=\(22\frac{2}{3}\)