Una fracción mixta es un número entero y una fracción propia representada juntos. Generalmente representa un número entre dos números enteros cualesquiera.
Las fracciones mixtas también se conocen como números mixtos.
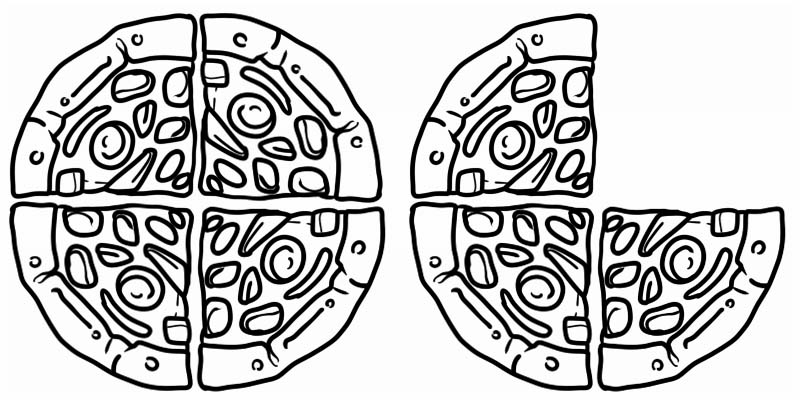
Mira la imagen dada, representa una fracción que es mayor que 1 pero menor que 2. Es, por lo tanto, un número mixto, igual a \(1\frac{3}{4}\)
Algunos otros ejemplos de números mixtos son:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Un número mixto se forma combinando tres partes: un número entero, un numerador y un denominador. El numerador y el denominador son parte de la fracción propia que forma el número mixto.
En el número mixto \(3\frac{1}{2}\)
Paso 1: Divide el numerador por el denominador
Paso 2: Escribe el cociente como el número entero
Paso 3: Escribe el resto como numerador y el divisor como denominador
Por ejemplo, seguimos los pasos dados para convertir \(\frac{7}{3}\) en una forma de número mixto.
Paso 1: divide 7 entre 3
Paso 2: Escribe el cociente, el divisor y el resto en forma de número mixto: \(2\frac{1}{3}\)
Uno puede sumar (o restar) números mixtos reorganizando los números enteros, sumando (o restando) por separado y sumando las fracciones sobrantes individualmente y al final combinándolos todos.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Sumar los números enteros por separado y las fracciones por separado.
Para números enteros:
1 + 3 = 4
Para fracciones: encuentra el MCM y luego suma
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Convirtiendo la fracción impropia en un número mixto: \(\frac{5}{4} = 1\frac{1}{4}\)
Al final, sumando ambas partes juntas.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Simplemente siga el mismo método (como para sumar), pero reste en lugar de sumar:
Ejemplo: \(15\frac{3}{4} - 8\frac{5}{6}\)
Convierte a fracciones impropias: \(\frac{63}{4} - \frac{53}{6}\)
El común denominador (mcm de 4 y 6) de 12: \(\frac{189}{12} - \frac{106}{12}\)
Ahora resta: \(\frac{83}{12}\)
Pasar a fracción mixta: \(6\frac{11}{12}\)
Ejemplo: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Ejemplo:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)