Une fraction mixte est un nombre entier et une fraction propre représentée ensemble. Il représente généralement un nombre compris entre deux nombres entiers.
Les fractions mixtes sont également appelées nombres mixtes.
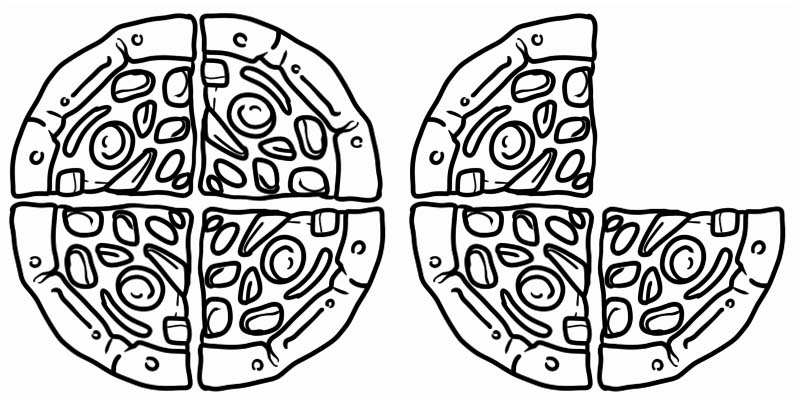
Regardez l'image donnée, elle représente une fraction supérieure à 1 mais inférieure à 2. C'est donc un nombre fractionnaire, égal à \(1\frac{3}{4}\)
Voici d'autres exemples de nombres mixtes :
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Un nombre fractionnaire est formé en combinant trois parties : un nombre entier, un numérateur et un dénominateur. Le numérateur et le dénominateur font partie de la fraction propre qui forme le nombre fractionnaire.
Dans le nombre mixte \(3\frac{1}{2}\)
Étape 1 : Divisez le numérateur par le dénominateur
Étape 2 : Écrivez le quotient sous la forme d'un nombre entier
Étape 3 : Notez le reste comme numérateur et le diviseur comme dénominateur
Par exemple, nous suivons les étapes données pour convertir \(\frac{7}{3}\) en une forme de nombre mixte.
Étape 1 : Divisez 7 par 3
Étape 2 : Écrivez le quotient, le diviseur et le reste sous la forme d'un nombre mixte : \(2\frac{1}{3}\)
On peut ajouter (ou soustraire) des nombres mixtes en réarrangeant les nombres entiers, en les ajoutant (ou en les soustrayant) séparément et en ajoutant les fractions restantes individuellement et à la fin en les combinant toutes.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Additionner les nombres entiers séparément et les fractions séparément.
Pour les nombres entiers :
1 + 3 = 4
Pour les fractions : trouvez le LCM, puis ajoutez
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Conversion de la fraction impropre en nombre fractionnaire : \(\frac{5}{4} = 1\frac{1}{4}\)
En fin de compte, en ajoutant les deux parties ensemble.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Suivez simplement la même méthode (comme pour l'addition), mais soustrayez au lieu d'ajouter :
Exemple : \(15\frac{3}{4} - 8\frac{5}{6}\)
Convertir en fractions impropres : \(\frac{63}{4} - \frac{53}{6}\)
Le dénominateur commun (LCM de 4 et 6) de 12 : \(\frac{189}{12} - \frac{106}{12}\)
Soustrayez maintenant : \(\frac{83}{12}\)
Changer en fraction mixte : \(6\frac{11}{12}\)
Exemple : \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Exemple:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)