मिश्रित भिन्न एक पूर्ण संख्या होती है, और एक उचित भिन्न को एक साथ प्रदर्शित किया जाता है। यह आम तौर पर किन्हीं दो पूर्ण संख्याओं के बीच की संख्या का प्रतिनिधित्व करता है।
मिश्रित भिन्न को मिश्रित संख्या भी कहते हैं।
दी गई छवि को देखें यह एक भिन्न का प्रतिनिधित्व करता है जो 1 से बड़ा है लेकिन 2 से कम है। इस प्रकार, यह एक मिश्रित संख्या है, जो \(1\frac{3}{4}\) के बराबर है।
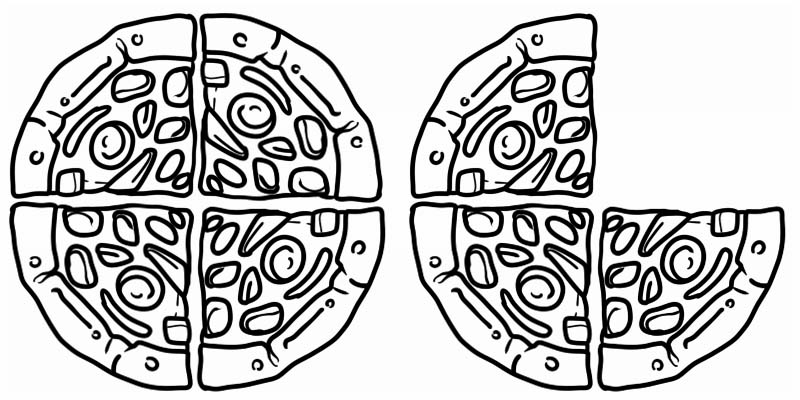
मिश्रित संख्याओं के कुछ अन्य उदाहरण हैं:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
एक मिश्रित संख्या तीन भागों को मिलाकर बनती है: एक पूर्ण संख्या, एक अंश और एक हर। अंश और हर उस उचित भिन्न का हिस्सा हैं जो मिश्रित संख्या बनाता है।
मिश्रित संख्या में \(3\frac{1}{2}\)
चरण 1: अंश को हर से विभाजित करें
चरण 2: भागफल को पूर्ण संख्या के रूप में लिखें
चरण 3: शेष को अंश के रूप में और भाजक को हर के रूप में लिखिए
उदाहरण के लिए, हम \(\frac{7}{3}\) को मिश्रित संख्या के रूप में बदलने के लिए दिए गए चरणों का पालन करते हैं।
चरण 1: 7 को 3 . से विभाजित करें
चरण 2: भागफल, भाजक और शेषफल को मिश्रित संख्या के रूप में लिखें: \(2\frac{1}{3}\)
पूर्ण संख्याओं को पुनर्व्यवस्थित करके, उन्हें अलग-अलग जोड़कर (या घटाकर) मिश्रित संख्याओं को जोड़ा (या घटाया जा सकता है) और बचे हुए अंशों को अलग-अलग जोड़कर और अंत में उन सभी को मिलाकर।
\(1\frac{1}{2} + 3\frac{3}{4} \)
पूर्ण संख्याओं को अलग-अलग और भिन्नों को अलग-अलग जोड़ना।
पूर्ण संख्याओं के लिए:
1 + 3 = 4
भिन्नों के लिए: LCM ज्ञात करें और फिर जोड़ें
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
अनुचित भिन्न को मिश्रित संख्या में बदलना: \(\frac{5}{4} = 1\frac{1}{4}\)
अंत में दोनों भागों को आपस में मिला दें।
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
बस उसी विधि का पालन करें (जैसे जोड़ने के लिए), लेकिन जोड़ने के बजाय घटाएं:
उदाहरण: \(15\frac{3}{4} - 8\frac{5}{6}\)
अनुचित भिन्नों में बदलें: \(\frac{63}{4} - \frac{53}{6}\)
12 का सामान्य हर (4 और 6 का एलसीएम): \(\frac{189}{12} - \frac{106}{12}\)
अब घटाएं: \(\frac{83}{12}\)
मिश्रित भिन्न में बदलें: \(6\frac{11}{12}\)
उदाहरण: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
उदाहरण:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)