Back to the topics list

mješovita frakcija, mješoviti brojevi

Što su miješani razlomci?

Mješoviti razlomak je cijeli broj, a pravi razlomak predstavljen zajedno. Općenito predstavlja broj između bilo koja dva cijela broja.

Mješoviti razlomci su također poznati kao mješoviti brojevi.

Pogledajte danu sliku predstavlja razlomak koji je veći od 1, ali manji od 2. Dakle, to je mješoviti broj, jednak \(1\frac{3}{4}\)

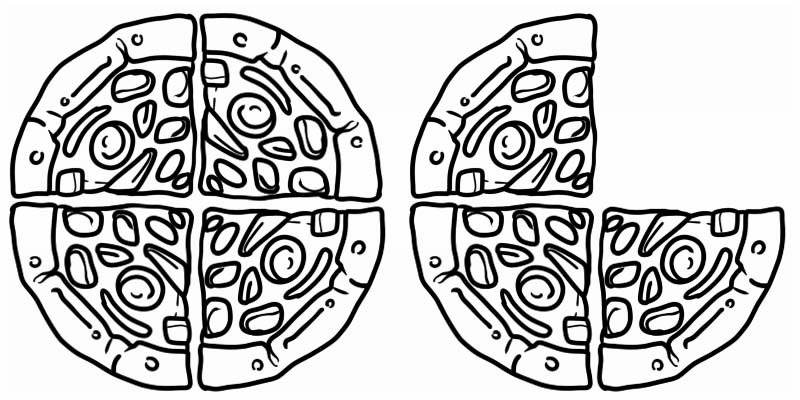
Neki drugi primjeri mješovitih brojeva su:

\(3\frac{1}{2}\)

\(2\frac{3}{5}\)

\(5\frac{3}{5}\)

\(4\frac{1}{5}\)

Dijelovi mješovitog broja

Mješoviti broj nastaje spajanjem tri dijela: cijelog broja, brojnika i nazivnika. Brojnik i nazivnik dio su pravog razlomka koji čini mješoviti broj.

U mješovitom broju \(3\frac{1}{2}\)

• 3 je cijeli broj
• \(\frac{1}{2}\) je razlomak, gdje je 1 brojnik, a 2 nazivnik

Svojstva mješovitih brojeva

• Djelomično je cijeli broj
• Djelomično je to razlomak

Pretvaranje nepravilnog razlomka u miješane razlomke

Korak 1: Podijelite brojnik s nazivnikom

Korak 2: Zapišite količnik kao cijeli broj

Korak 3: Ostatak zapišite kao brojnik, a djelitelj kao nazivnik

Na primjer, slijedimo navedene korake da pretvorimo \(\frac{7}{3}\) u mješoviti broj.

Korak 1: Podijelite 7 sa 3

Korak 2: Napišite kvocijent, djelitelj i ostatak u obliku mješovitog broja: \(2\frac{1}{3}\)

Dodavanje ili oduzimanje miješanih razlomaka

Može se zbrajati (ili oduzimati) mješoviti brojevi preuređivanjem cijelih brojeva, zbrajanjem (ili oduzimanjem) zasebno i dodavanjem preostalih razlomaka pojedinačno i na kraju ih sve kombinirajući.

\(1\frac{1}{2} + 3\frac{3}{4} \)

Zbrajanje cijelih brojeva zasebno i razlomaka zasebno.

Za cijele brojeve:

1 + 3 = 4

Za razlomke: Pronađite LCM i zatim dodajte

\(\frac{1}{2} + \frac{3}{4}\)

= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)

= \(\frac{2}{4} + \frac{3}{4}\)

= \(\frac{5}{4}\)

Pretvaranje nepravilnog razlomka u mješoviti broj: \(\frac{5}{4} = 1\frac{1}{4}\)

Na kraju, zbrajanje oba dijela zajedno.

\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)

Oduzimanje mješovitih razlomaka

Samo slijedite istu metodu (kao za dodavanje), ali oduzmite umjesto dodavanja:

Primjer: \(15\frac{3}{4} - 8\frac{5}{6}\)

Pretvori u nepravilne razlomke: \(\frac{63}{4} - \frac{53}{6}\)

Zajednički nazivnik (LCM od 4 i 6) od 12: \(\frac{189}{12} - \frac{106}{12}\)

Sada oduzmite: \(\frac{83}{12}\)

Promijeni u mješoviti razlomak: \(6\frac{11}{12}\)

Množenje mješovitih razlomaka

• Promijenite svaki miješani razlomak u nepravilan razlomak
• Pojednostavite ako je moguće
• Pomnožite brojnike, a zatim nazivnike
• Odgovorite najnižim riječima
• Provjerite je li odgovor razuman

Primjer: \(5\frac{2}{3} \times \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{1}{4}\)

= \(\frac{17}{12}\)

= \(1\frac{5}{12}\)

Dijeljenje miješanih frakcija

• Promijenite svaki miješani razlomak u nepravilan razlomak
• Pomnožite s recipročnom vrijednosti djelitelja, pojednostavljujući ako je moguće
• Odgovorite najnižim riječima
• Provjerite je li odgovor razuman

Primjer:

\(5\frac{2}{3} \div \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{4}{1}\)

= \(\frac{68}{3}\)

= \(22\frac{2}{3}\)