Una frazione mista è un numero intero e una frazione propria rappresentata insieme. Generalmente rappresenta un numero compreso tra due numeri interi qualsiasi.
Le frazioni miste sono anche conosciute come numeri misti.
Guarda l'immagine data rappresenta una frazione che è maggiore di 1 ma minore di 2. È quindi un numero misto, uguale a \(1\frac{3}{4}\)
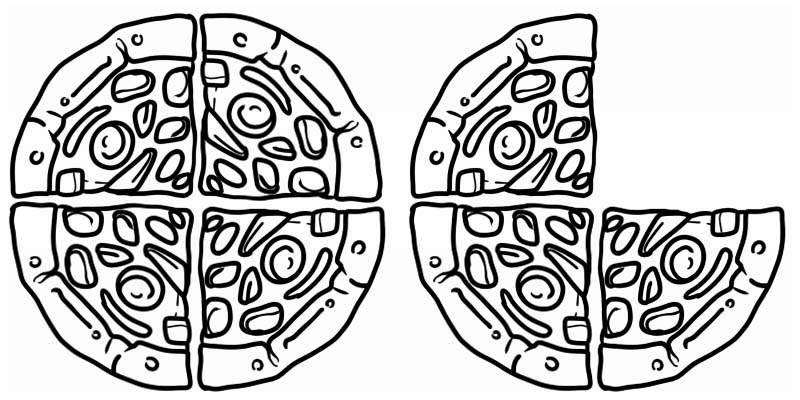
Alcuni altri esempi di numeri misti sono:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Un numero misto si forma combinando tre parti: un numero intero, un numeratore e un denominatore. Il numeratore e il denominatore fanno parte della frazione propria che compone il numero misto.
Nel numero misto \(3\frac{1}{2}\)
Passaggio 1: dividi il numeratore per il denominatore
Passaggio 2: annota il quoziente come numero intero
Passo 3: Scrivi il resto come numeratore e il divisore come denominatore
Ad esempio, seguiamo i passaggi indicati per convertire \(\frac{7}{3}\) in una forma numerica mista.
Passaggio 1: dividi 7 per 3
Passo 2: Scrivi quoziente, divisore e resto nella forma numerica mista: \(2\frac{1}{3}\)
Si possono sommare (o sottrarre) numeri misti riordinando i numeri interi, sommandoli (o sottraendoli) separatamente e sommando le frazioni rimanenti singolarmente e infine combinandole tutte.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Sommando i numeri interi separatamente e le frazioni separatamente.
Per i numeri interi:
1 + 3 = 4
Per le frazioni: Trova il MCM e poi aggiungi
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Conversione della frazione impropria in un numero misto: \(\frac{5}{4} = 1\frac{1}{4}\)
Alla fine, sommando entrambe le parti insieme.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Basta seguire lo stesso metodo (come per l'addizione), ma sottrarre invece di aggiungere:
Esempio: \(15\frac{3}{4} - 8\frac{5}{6}\)
Converti in frazioni improprie: \(\frac{63}{4} - \frac{53}{6}\)
Il comune denominatore (LCM di 4 e 6) di 12: \(\frac{189}{12} - \frac{106}{12}\)
Ora sottrai: \(\frac{83}{12}\)
Trasforma in una frazione mista: \(6\frac{11}{12}\)
Esempio: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Esempio:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)