帯分数は整数と固有分数を合わせて表したものです。通常、任意の 2 つの整数の間の数値を表します。
帯分数は帯分数とも呼ばれます。
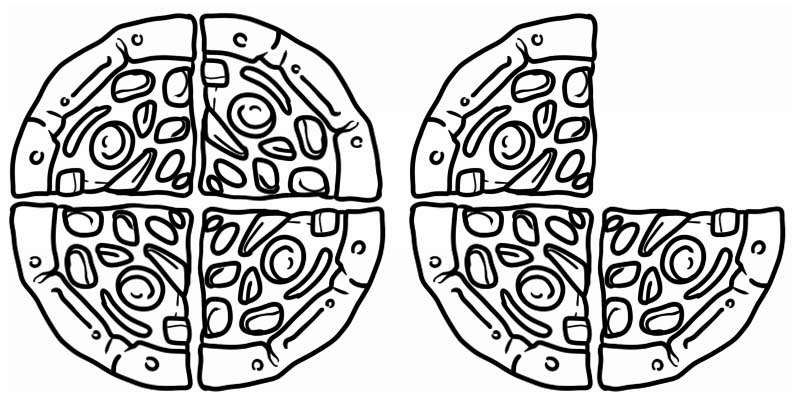
与えられた画像を見てください。これは 1 より大きく 2 より小さい分数を表しています。したがって、 \(1\frac{3}{4}\)に等しい混合数です。
混合数の他の例は次のとおりです。
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
混合数は、整数、分子、分母の 3 つの部分を組み合わせて形成されます。分子と分母は、帯分数を作る適切な分数の一部です。
混合数\(3\frac{1}{2}\)
ステップ 1: 分子を分母で割る
ステップ 2: 商を整数として書き留める
ステップ 3: 剰余を分子、除数を分母として書き留めます。
たとえば、与えられた手順に従って\(\frac{7}{3}\)を混合数形式に変換します。
ステップ 1: 7 を 3 で割る
ステップ 2: 商、除数、剰余を混合数形式で書きます: \(2\frac{1}{3}\)
整数を並べ替え、それらを別々に加算 (または減算) し、残りの分数を個別に加算し、最後にそれらすべてを結合することによって、混合数を加算 (または減算) することができます。
\(1\frac{1}{2} + 3\frac{3}{4} \)
整数を別々に足し、分数を別々に足す。
整数の場合:
1 + 3 = 4
分数の場合: 最小公倍数を見つけて追加します
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
仮分数を帯分数に変換: \(\frac{5}{4} = 1\frac{1}{4}\)
最後に、両方のパーツを一緒に追加します。
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
同じ方法 (加算と同様) に従いますが、加算ではなく減算を行います。
例: \(15\frac{3}{4} - 8\frac{5}{6}\)
仮分数に変換: \(\frac{63}{4} - \frac{53}{6}\)
12 の共通分母 (4 と 6 の最小公倍数): \(\frac{189}{12} - \frac{106}{12}\)
減算: \(\frac{83}{12}\)
帯分数に変更: \(6\frac{11}{12}\)
例: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
例:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)